Trong không gian Oxyz, cho mặt cầu (S): (x-3)^2+(y-2)^2

Đáp án B

Mặt cầu \[\left( S \right)\] có tâm \[I\left( {3;2;0} \right)\] và bán kính \[R = 2\].

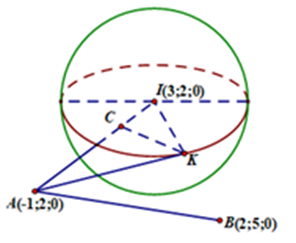
Ta có \[\overrightarrow {AI} = \left( {4;0;0} \right) \Rightarrow AI = 4 \Rightarrow AI = 2IK \Rightarrow \frac{{IA}}{{IK}} = 2\].

Trên đoạn thẳng AI lấy điểm C sao cho \[IC = 1 \Rightarrow C\] cố định.

Ta có \[\begin{array}{l}IC.IA = 1.4 = 4 = I{K^2} \Rightarrow \Delta ICK\~\Delta IKA\\ \Rightarrow \frac{{CK}}{{KA}} = \frac{{IK}}{{IA}} = \frac{1}{2} \Rightarrow KA = 2KC\end{array}\]

\[ \Rightarrow KA + 2KB = 2\left( {KC + KB} \right) \ge 2BC\] (không đổi).

Dấu “=” xảy ra \[ \Leftrightarrow K = BC \cap \left( S \right)\] và K ở giữa B và C.

Ta có \[\overrightarrow {IA} = 4\overrightarrow {IC} \Rightarrow C\left( {2;2;0} \right)\].

Đường thẳng BC qua \[C\left( {2;2;0} \right)\] và nhận \[\overrightarrow {CB} = \left( {0;3;0} \right)\] là một VTCP.

\[ \Rightarrow BC:\left\{ \begin{array}{l}x = 2\\y = 2 + 2t\\z = 0\end{array} \right. \Rightarrow K\left( {2;2t + 2;0} \right)\].

Ép cho \[K \in \left( S \right) \Rightarrow 1 + 4{t^2} = 4 \Rightarrow t = \pm \frac{{\sqrt 3 }}{2} \Rightarrow \left[ \begin{array}{l}K\left( {2;2 + \sqrt 3 ;0} \right)\\K\left( {2;2 - \sqrt 3 ;0} \right)\end{array} \right.\].

Mà K ở giữa B và C \[ \Rightarrow K\left( {2;2 + \sqrt 3 ;0} \right)\].