Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = a, SB = a căn 2

* Hướng dẫn giải

Đáp án D

Phương pháp:

- Gọi H là trực tâm tam giác, chứng minh $SH\perp \left(ABC\right)$ bằng cách sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”.

- Tính độ dài SH bằng cách sử dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông.

Cách giải: Gọi H là trực tâm của tam giác ABC.

Ta sẽ chứng minh SH là đường cao của hình chóp.

Gọi E, D lần lượt là hình chiếu của B,A lên AC,BC.

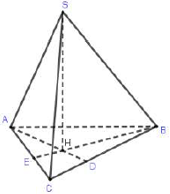
Chú ý khi giải: Từ nay về sau, các em có thể ghi nhớ hệ thức liên hệ giữa đường cao và cạnh trong hình chóp S.ABC mà có SA, SB, SC đôi một vuông góc, đó là $\frac{1}{S{H}^2}=\frac{1}{S{A}^2}\frac{1}{S{B}^2}+\frac{1}{S{C}^2}$