Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1)

* Hướng dẫn giải

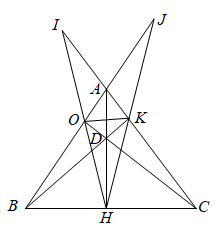
Ta có tứ giác BOKC là tứ giác nội tiếp đường tròn suy ra $\widehat{OKB}=\widehat{OCB } \left(1\right)$

Ta có tứ giác KDHC là tứ giác nội tiếp đường tròn suy ra $\widehat{DKH}=\widehat{OCB} \left(2\right)$

Do đó BK là đường phân giác trong của góc $\widehat{OKH}$ và AC là đường phân giác ngoài của góc $\widehat{OKH}$.

Tương tự ta chứng minh được OC là đường phân giác trong của góc  $\widehat{KOH}$ và AB là đường phân giác ngoài của góc $\widehat{KOH}$

Chọn D