Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết !!
Trong không gian với hệ tọa độ Oxyz, cho đường...
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng denta: (x+1)
Câu hỏi :
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và hai điểm . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi là giao điểm của d với đường thẳng . Giá trị bằng
A. -2
B. 4
C. 2
D. 6
* Đáp án
* Hướng dẫn giải

- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
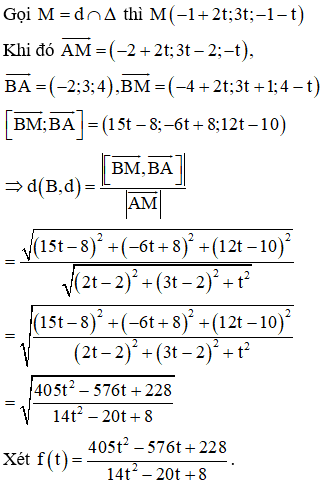
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN tại t = 2)
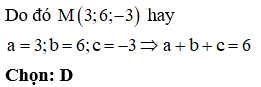
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết !!
Số câu hỏi: 1882
Copyright © 2021 HOCTAP247
