Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Cho hai hình vuông có cạnh đều bằng 5 được...
Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho
Câu hỏi :
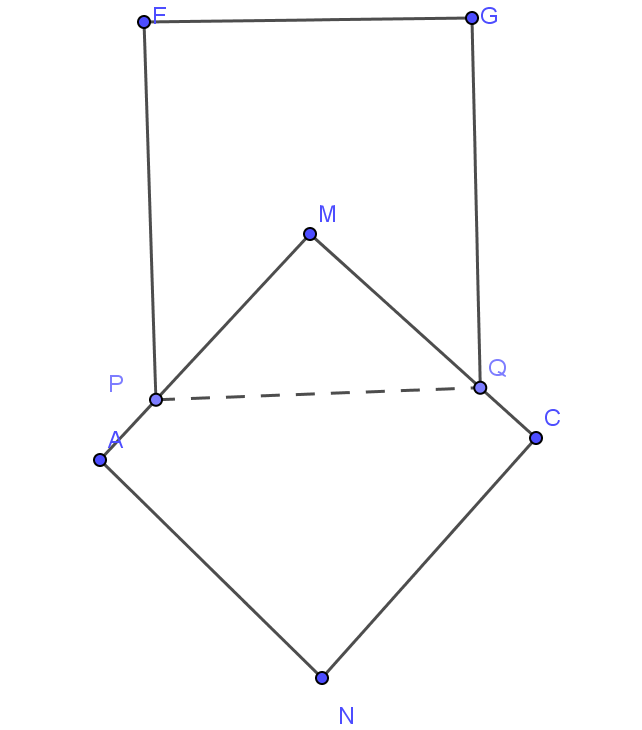
Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho đỉnh M của hình vuông này là tâm của hình vuông kia, đường chéo MN vuông góc với cạnh PQ tạo thành hình phẳng (H) ( như hình vẽ bên).
A.
B.
C.
D.
* Đáp án
A
* Hướng dẫn giải
Đáp án A.
Gọi là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy và đường cao = EP = 5 =>
Gọi là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy Đường cao =>
Gọi là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy đường cao =>
Ta có thể tích của toàn khối tròn xoay
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
