Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm

* Hướng dẫn giải

Đáp án D

Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.

Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.

Để tính diện tích MNP, ta cần đi tìm MG và NP.

Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó 

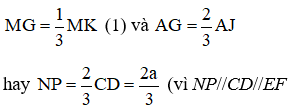
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).

Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là