Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Cho tứ diện đều ABCD có cạnh 2a. Tính bán...
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt
Câu hỏi :
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện
A.
B.
C.
D.
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Gọi H và K lần lượt là hình chiếu của A xuống (BCD) và (ABC).
Khi đó O là tâm mặt cầu nội tiếp tứ diện
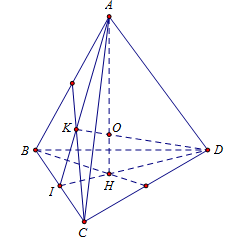
Ta có:
Ta có:
Cách 2: Ta có:
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
