Cho hình chóp S.ABC có AB=BC=CA=a, SA=SB=SC=a căn3

* Hướng dẫn giải

Đáp án C

Gọi E và F là trung điểm của BC và AB và O là trọng tâm tam giác ABC ta có: $SO\perp \left(ABC\right)$

Do $\left\{\begin{array}{l}AE=BC\\ SO=BC\end{array}\right.\Rightarrow BC\perp \left(SAE\right)$. Dựng $EK\perp A$ suy ra EK là đoạn vuông góc cung của SA và BC. Tương tự dựng FI; RL là các đoạn vuông góc chung của 2 cạnh đối diện.

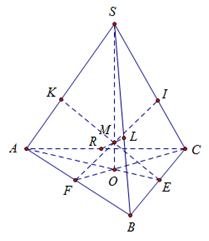
Do tính chất đối xứng ta dễ dàng suy ra EK, FI, RL đồng quy tại điểm M

Như vậy $d\ge EK+FI+RL=3EK$

Mặc khác $OA=\frac{a\sqrt{3}}{3}\Rightarrow \cos \stackrel{⏜}{SAO}=\frac{1}{3}\Rightarrow \sin \stackrel{⏜}{SAO}=\frac{2\sqrt{2}}{3}$

Do đó: $KE=AE\sin A=\frac{a\sqrt{3}}{2}-\frac{2\sqrt{2}}{3}=\frac{a\sqrt{6}}{3}$

Do vậy $d_{\min }=a\sqrt{6}$