Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a

* Hướng dẫn giải

Đáp án D

Phương pháp:

- Tìm một mặt phẳng chứa SK mà song song với MN, đó chính là mặt phẳng (SAD)

- Từ đó ta chỉ cần tính khoảng cách từ MN đến (SAD).

Cách giải: Gọi I là trung điểm AD, AC cắt BD tại O. H là hình chiếu vuông góc của O trên SI.

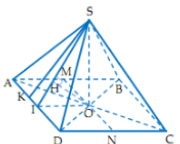
Chú ý khi giải: HS thường không chú ý đến phương pháp tìm mặt phẳng song song mà chỉ tập trung đi tìm đường vuông góc chung dẫn đến sự phức tạp cho bài toán và không đi đến được đáp án.