Cho hàm số (C): y=x^3+3x^2+1 .Đường thẳng đi qua điểm A(-3;1)

* Hướng dẫn giải

Đáp án C

Phương pháp:

Viết phương trình đường thẳng đi qua A và có hệ số góc k .

Biện luận số giao điểm của hai đồ thị là số nghiệm của phương trình hoành độ giao điểm để suy ra kết luận.

Cách giải:

Xét hàm số: $y=x^3+3x^2+1\left(C\right)$ trên R

Ta có: $y\text{'}=3x^2+6x;y\text{'}=0\iff 3x^2+6x=0\iff \left[\begin{array}{l}x=0\\ x=-2\end{array}\right.$

Ta có (C) là hàm số bậc 3 xác định trên R, đồ thị của nó có duy nhất 2 cực trị hoặc không có điểm cực trị nào.

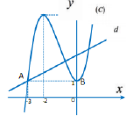
Ta có: $a=1>0\to B\left(0;1\right)$ là điểm cực tiểu của (C).

Ta có: $\overrightarrow{AB}=\left(3;0\right)\Rightarrow AB//Ox$

=> để thỏa mãn yêu cầu bài toán thì điều kiện cần là k>0 với k là hệ số góc đường thẳng cắt (C) tại 3 điểm phân biệt

Gọi $d:y=kx+a$ với: $k>0;k,a\in R$

Ta lại có 

$A\left(-3;1\right)\in d\Rightarrow 1=-3k+a\iff a=1+3k$

$\Rightarrow d:y=kx+3k+1$

d cắt (C) tại 3 điểm phân biệt

<=> phương trình: $kx+3k+1=x^3+3x^2+1\left(1\right)$có 3 nghiệm phân biệt.

Phương trình $\left(1\right)\iff \left(x+3\right)\left(x^2-k\right)=0$$\iff \left[\begin{array}{l}x=-3\\ x=\pm \sqrt{k}\end{array}\right.$vì k>0

Để phương trình (1) có 3 nghiệm phân biệt

Vậy $k>0;k\ne 9$ thỏa mãn yêu cầu của bài.

Chú ý khi giải:

HS cần chú ý cách viết phương trình đường thẳng đi qua 1 điểm và có hệ số góc.

Liên hệ được mối liên hệ giữa số giao điểm và số nghiệm của phương trình để biện luận.