Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Cho hình chóp tứ diện đều S.ABCD có canh đáy...
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp
Câu hỏi :
Cho hình chóp tứ diện đều S.ABCD có canh đáy a, cạnh bên hợp với đáy một góc . Gọi M là điểm đối xứng với C qua D, N là trung điểm của SC, mặt phẳng (BMN) chia khối chóp S.ABCD thành 2 phần. Tính tỉ số thể tích của hai phần đó.
A.
B.
C.
D.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
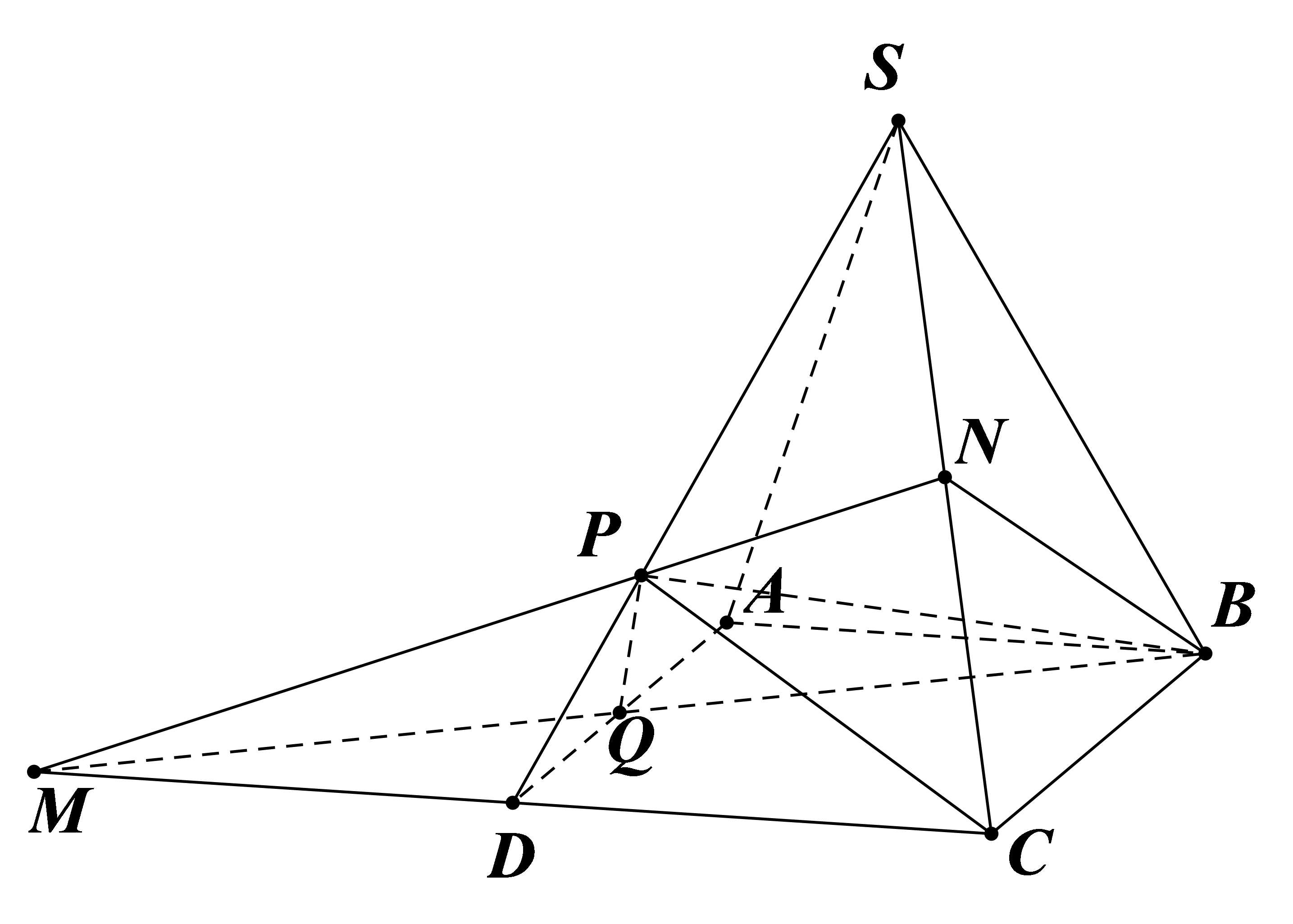
Áp dụng định lí Menelaus cho ta có:
.
Ta có:
.
Do đó .
Vậy tỉ số thể tích của 2 phần cần tìm là .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
