Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Cho tứ diện ABCD có AB=AD=a căn 2 , BC=BD=a...
Cho tứ diện ABCD có AB=AD=a căn 2 , BC=BD=a và CA=CD=x .
Câu hỏi :
Cho tứ diện ABCD có , và . Khoảng cách từ B đến mặt phẳng (ACD) bằng . Biết thể tích của khối tứ diện bằng . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
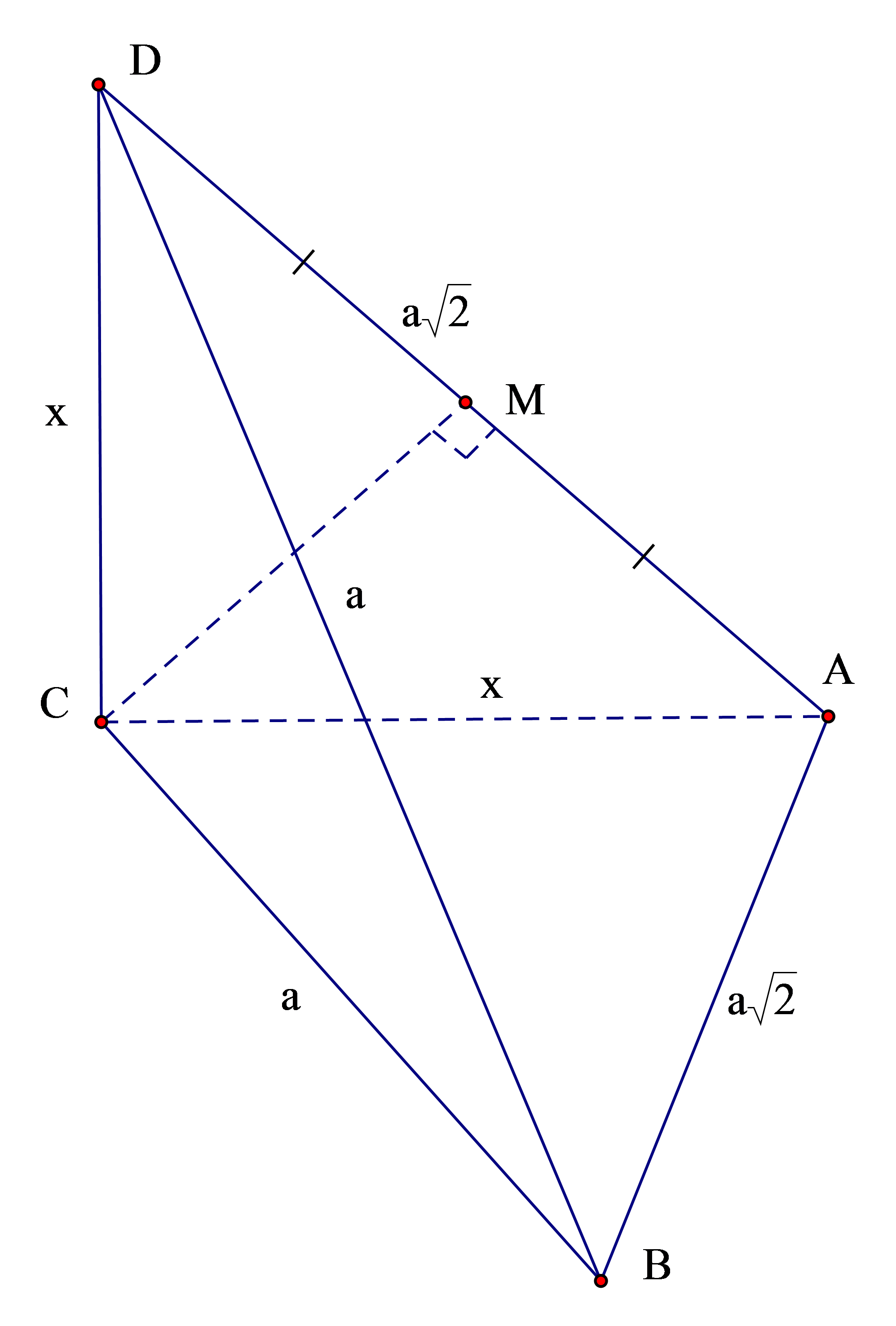
Gọi h là khoảng cách từ
Gọi M là trung điểm AD.
vuông tại
Hay góc giữa hai mặt phẳng bằng
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp 20 đề thi thử THPTQG môn Toán cực hay có đáp án !!
Số câu hỏi: 1000
Copyright © 2021 HOCTAP247
