Cho hình chóp tứ giác đều S.ABCD có SA=a và góc SAB=11pi/24.

* Hướng dẫn giải

Đáp án C

Trải khối chóp đều S.ABCD ra mặt phẳng như hình vẽ bên:

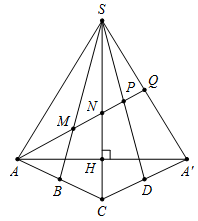
Với điểm A=A' và H là trung điểm của AA'

Dễ thấy để $AM+MN+NP+PQ$ nhỏ nhất <=> các điểm A, M, N, P, Q thẳng hàng $\Rightarrow AM+MN+NP+PQ=AQ$

Tam giác SAA' có $\stackrel{⏜}{ASA}=4\stackrel{⏜}{ASB}=4\left(\pi -2\frac{11\pi }{24}\right)=\frac{\pi }{3}$

Mà $SA=SA\text{'}\Rightarrow \Delta SAA\text{'}$ là tam giác đều $\Rightarrow AQ=\frac{a\sqrt{3}}{2}$