Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, AB=8 SA=SB=6 . Gọi

* Hướng dẫn giải

Đáp án D

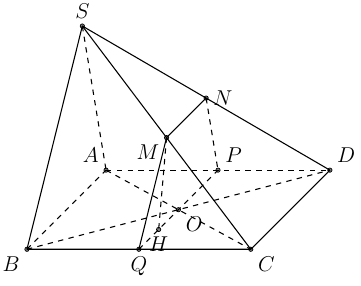
Qua O dựng đường thẳng$PQ\parallel AB$. Vậy P, Q lần lượt là trung điểm của AD và BC.

Qua P dựng đường thẳng$PN\parallel SA$. Vậy N là trung điểm của SD

Qua Q dựng đường thẳng$QM\parallel SB$. Vậy M là trung điểm của SC.

Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.

Vì $PQ\parallel CD,MN\parallel CD\Rightarrow PQ\parallel MN$. Vậy tứ giác MNPQ là hình thang.

Ta có $PQ=AB=8\text{\$},MN=\frac{1}{2}AB=\mathrm{4,}MQ=NP=\frac{1}{2}SA=3$. Vậy MNPQ là hình thang cân.

Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có 

$$\begin{gathered} HQ=\frac{1}{4}PQ=2 \\ \Rightarrow MH=\sqrt{M{Q}^2-H{Q}^2}=\sqrt{5} \end{gathered}$$

Vậy diện tích của thiết diện cần tìm là $S=\frac{(MN+PQ)MH}{2}=6\sqrt{5}.$