Cho hình chóp ?.????có đáy là hình thoi tâm O cạnh a, góc ABC= 60 độ ,SA=SB=SC=2a . Tính khoảng

* Hướng dẫn giải

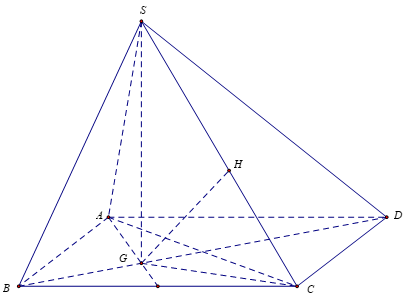
Từ giả thiết suy ra: hình chóp S.ABC là hình chóp đều.

Gọi G là trọng tâm tam giác $ABC\Rightarrow SG\perp \left(ABCD\right)$

$$\begin{gathered} AB//CD\Rightarrow AB//\left(SCD\right) \\ \Rightarrow d\left(AB;SC\right)=d\left(AB;\left(SCD\right)\right) \\ =d\left(B;\left(SCD\right)\right)=\frac{3}{2}d\left(G;\left(SCD\right)\right) \end{gathered}$$ 

(Vì $\frac{BD}{GD}=\frac{3}{2}$).

Trong mp (ABCD) vẽ $GC\perp CD,CD\perp SG$ $\Rightarrow CD\perp \left(SGC\right)\Rightarrow \left(SGC\right)\perp \left(SCD\right)$

Mà $\left(SGC\right)\cap \left(SCD\right)=SC$, vẽ $GH\perp SC$ $\Rightarrow d\left(G;\left(SCD\right)\right)=GH$

$GB=GC=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$.

$\Rightarrow SG=\sqrt{S{B}^2-B{G}^2}=\sqrt{4a^2-\frac{a^2}{3}}=\frac{a\sqrt{11}}{\sqrt{3}}$

Tam giác SHG vuông tại G: 

$$\begin{gathered} \frac{1}{G{H}^2}=\frac{1}{S{G}^2}+\frac{1}{G{C}^2}=\frac{3}{11a^2}+\frac{3}{a^2}=\frac{36}{11a^2} \\ \Rightarrow GH=\frac{a\sqrt{11}}{6} \end{gathered}$$

Vậy $d\left(AB;SC\right)=\frac{a\sqrt{11}}{4}$