Trong không gian với hệ trục tọa độ Oxyz, cho A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c dương

* Hướng dẫn giải

Đáp án D.

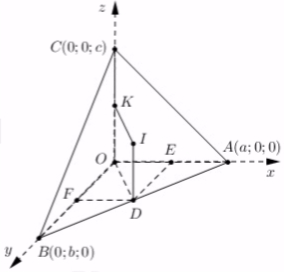
Gọi D, K lần lượt là trung điểm của AB, OC. Từ D kẻ đường  thẳng vuông góc với mặt phẳng (OAB). Và cắt mặt phẳng trung trực của OC tại $I\Rightarrow I$ là tâm mặt cầu ngoại tiếp tứ diện OABC suy ra $z_1=\frac{c}{2}$. 

Ta có $S_{∆OAD}=\frac{1}{2}.S_{∆OAB}=\frac{1}{4}.ab=\frac{1}{2}.DE.OA\Rightarrow DE=\frac{b}{2}$. 

Tương tự $DF=\frac{a}{2}\Rightarrow x_1=\frac{a}{2},y=\frac{b}{2}\Rightarrow I\left(\frac{a}{2};\frac{b}{2};\frac{c}{2}\right)$. 

Suy ra $x_1+y_1+z_1=\frac{a+b+c}{2}=1\Rightarrow I\in \left(P\right):x+y+z-1=0$. 

Vậy khoảng cách từ điểm M dến (P) bằng $d=\frac{2015}{\sqrt{3}}$.