Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Cho hình chữ nhật ABCD có AB = 2a, BC...
Cho hình chữ nhật ABCD có AB = 2a, BC = 3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA = 2MD, NB = 2NC
Câu hỏi :
Cho hình chữ nhật ABCD có AB = 2a, BC = 3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA = 2MD, NB = 2NC. Khi quay quanh AB, các đường gấp khúc AMNB, ADCB sinh ra các hình trụ có diện tích toàn phần Tính tỉ số là:
A.
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Đáp án D
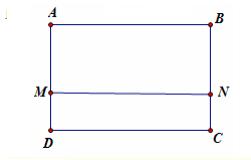 Hình trụ khi quay đường gấp khúc AMNB quanh AB có bán kính đáy là .
Hình trụ khi quay đường gấp khúc AMNB quanh AB có bán kính đáy là .
Tương tự
Khi đó .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Số câu hỏi: 737
Copyright © 2021 HOCTAP247
