Trong không gian với hệ tọa độ Oxyz , cho hai mặt cầu (P): x^2+y^2+z^2+4x+2y+z=0 và (Q): x^2+y^2+z^2-2x-y-z=0 cắt nhau

* Hướng dẫn giải

Đáp án A

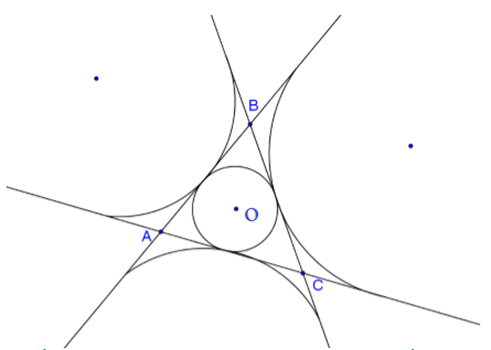
Ba điểm A,B,C tạo thành một tam giác. Có 4 đường tròn tiếp xúc với cả ba đường thẳng AB,AC,BC (hình vẽ trên).

Mặt cầu (S) cần tìm tiếp xúc với 3 đường thẳng AB,AC,BC, do đó nó phải chứa 1 trong 4 đường tròn trên.

Xét với 1 đường tròn bất kì trong 4 đường tròn trên, giả sử là đường tròn tâm (O) nằm bên trong tam giác, ta có:

Tâm I của mặt cầu (S) phải nằm trên đường thẳng d đi qua tâm O và vuông góc với (ABC). Mặt khác, I thuộc mp (P) chứa (C), (C) lại không vuông góc với (ABC) do đó chỉ có 1 giao điểm của d với (P). Tương tự, với 3 đường tròn còn lại, với mỗi đường tròn ta tìm được 1 tâm I nữa. Vậy có 4 mặt cầu thỏa mãn yêu cầu.