Cho hình chóp S.ACBD có đáy ABCD là hình vuông cạnh ,??⊥???? và??=?. Tìm

* Hướng dẫn giải

Đáp án D

Hạ H, K lần lượt là hình chiếu vuông góc của A xuống SB và SD.

Ta có:

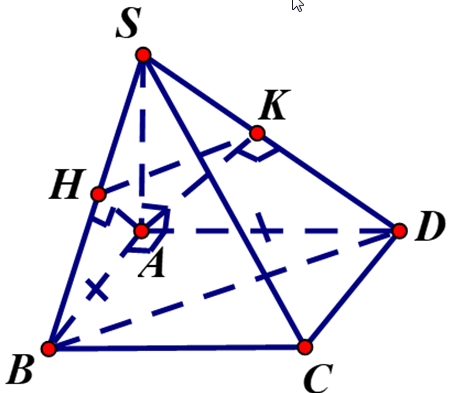
$\left.\begin{array}{l}AH\perp SB\\ AH\perp BC\end{array}\right\}\Rightarrow AH\perp \left(SBC\right)$. Tương tự $AK\perp \left(SDC\right)$

Như vậy $\widehat{\left(\left(SBC\right),\left(SDC\right)\right)}=\widehat{\left(AH,AK\right)}=\widehat{HAK}$

Ta có $\text{Δ}SAB=\text{Δ}SAD$ suy ra $AH=AK$. Vì góc giữa hai mặt phẳng (SBC) và (SCD) bằng ${60}^0$ nên ΔAHK đều.

Ta có $\frac{SH}{SB}=\frac{SK}{SD}=\frac{HK}{BD}$, mà $\frac{SH}{SB}=\frac{S{A}^2}{S{B}^2}=\frac{x^2}{x^2+a^2}=\frac{KH}{a\sqrt{2}}$ suy ra $KH=\frac{a\sqrt{2}{x}^2}{x^2+a^2}$.

Ta lại có $\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{B}^2}=\frac{a^2+x^2}{a^2{x}^2}$ suy ra $A{H}^2=\frac{a^2{x}^2}{a^2+x^2}$.

ΔAHK đều nên ta có

$$\begin{gathered} K{H}^2=A{H}^2\iff {\left(\frac{a\sqrt{2}{x}^2}{x^2+a^2}\right)}^2=\frac{a^2{x}^2}{a^2+x^2} \\ \iff x=a \end{gathered}$$.

Vậy $x=a$ thì góc giữa hai mặt phẳng (SBC) và (SCD) bằng ${60}^0$.