Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp đề thi thptqg môn Toán hay nhất !!
Cho tứ diện OABC có OA,OB,OC đội một vuông góc,...
Cho tứ diện OABC có OA,OB,OC đội một vuông góc, ??=?,??=?,??=?. Tính khoảng cách
Câu hỏi :
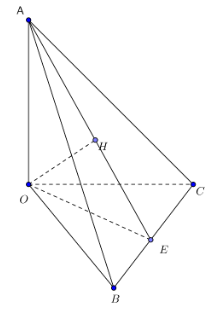
Cho tứ diện OABC có OA,OB,OC đội một vuông góc, . Tính khoảng cách d từ O tới mặt phẳng (ABC).
A.
B.
C.
D.
* Đáp án
A
* Hướng dẫn giải
Đáp án A
Gọi H là hình chiếu của O lên mặt phẳng (ABC) nên .
Mặt khác .
Từ (1),(2) suy ra . Chứng minh tương tự ta được. Suy ra H là trực tâm của ΔABC.
Trong mặt phẳng (ABC) gọi E là giao điểm của AH và BC.
Ta có tại H.
tức là OH là đường cao của tam giác vuông OAE.
Mặt khác OE là đường cao của tam giác vuông OBC.
Do đó: .
.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp đề thi thptqg môn Toán hay nhất !!
Số câu hỏi: 354
Copyright © 2021 HOCTAP247
