Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác...
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A, AB = a
Câu hỏi :
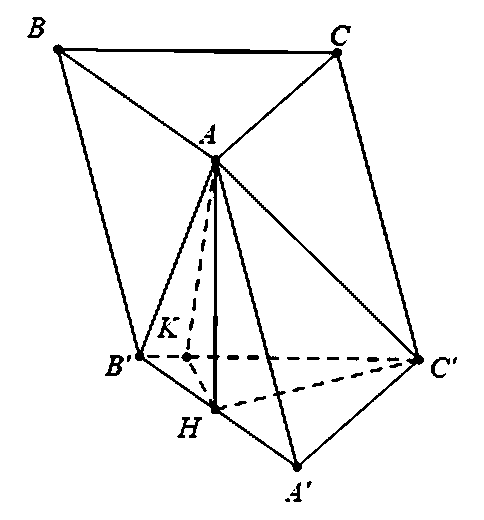
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A, AB = a, AC = . Biết góc giữa hai mặt phẳng (AB'C') và (ABC) bằng và hình chiếu của A lên (A'B'C') là trung điểm H của đoạn thẳng A'B'. Tính bán kính mặt cầu ngoại tiếp tứ diện A.HB'C' theo a
A.
B.
C.
D.
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Do góc giữa hai mặt phẳng (AB'C') và (ABC) bằng
Suy ra
Dựng , do
Do đó
 Mặt khác
Mặt khác
Suy ra
Do
Áp dụng công thức tính nhanh .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Số câu hỏi: 737
Copyright © 2021 HOCTAP247
