Trang chủ
Đề thi & kiểm tra
Toán học
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Cho hàm số y = f(x) = ax^3 + bx^2...
Cho hàm số y = f(x) = ax^3 + bx^2 + cx + d (a,b,c thuộc R, a khác 0) có đồ thị (C). Biết rằng đồ thị C tiếp xúc với đường thẳng
Câu hỏi :
Cho hàm số có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.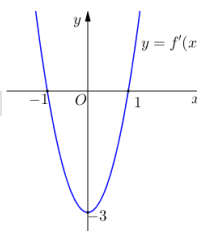 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
A. S = 9
B.
C.
D.
* Đáp án
D
* Hướng dẫn giải
Đáp án D
Dựa vào đồ thị hàm số
Khi đó .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
(Do x < 0 suy ra
Cho hoành độ các giao điểm là x = -2,x = 1
Khi đó .
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp đề thi THPTQG môn Toán cực hay, có lời giải chi tiết !!
Số câu hỏi: 737
Copyright © 2021 HOCTAP247
