Cho số phức z thỏa 4Iz + iI + 3Iz - iI = 10. Giá trị nhỏ nhất của IzI bằng

* Hướng dẫn giải

Đáp án D

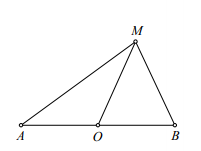Hình vẽ minh họa

Gọi A(0;-1);B(0;1) có trung điểm là O(0;0). Điểm M biểu diễn số phức z

Theo công thức trung tuyến trong tam giác MAB thì ${\left|z\right|}^2=M{O}^2=\frac{M{A}^2+M{B}^2}{2}-\frac{A{B}^2}{4}$ 

Theo giả thiết, ta có 4MA + 2MB = 10. 

Đặt $MA=t\Rightarrow MB=\frac{10-4t}{3}$ 

Vì $\left|MA-MB\right|=\frac{\left|10-7t\right|}{2}\le AB=2\Rightarrow -6\le 10-7t\le 6\iff a\in \left[\frac{4}{7};\frac{16}{7}\right]$ 

Ta có $M{A}^2+M{B}^2=t^2+{\left(\frac{10-4t}{3}\right)}^2=\frac{25t^2-80t+100}{9}=\frac{{\left(5t-8\right)}^2+36}{9}$ 

Do $-\frac{36}{7}\le 5t-8\le \frac{34}{7}\Rightarrow 0\le {\left(5t-8\right)}^2\le \frac{1296}{49}\Rightarrow M{A}^2+M{B}^2\ge 4$ nên ${\left|z\right|}^2\ge 1\Rightarrow m={\left|z\right|}_{min}=1$.