Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;6;2), B(3;0;0)

* Hướng dẫn giải

Đáp án B

Cách 1: Gọi I(a;b;c) là tâm của mặt cầu (S), vì $I\in \left(P\right)\Rightarrow I(a;a+2;c)$ 

Ta có $R=IA=IB\iff {\left(a-1\right)}^2+{\left(a-4\right)}^2+{\left(c-2\right)}^2={\left(a-3\right)}^2+{\left(a+2\right)}^2+c^2\iff c=2-2a$ 

Khi đó $R=IA=\sqrt{{\left(a-1\right)}^2+{\left(a-4\right)}^2+4a^2}=\sqrt{6a^2-10a+17}=\sqrt{6{\left(x-\frac{5}{6}\right)}^2+\frac{77}{6}}\ge \frac{\sqrt{462}}{6}$

Vậy bán kính nhỏ nhất của mặt cầu (S) là $R_{min}=\frac{\sqrt{462}}{6}$ 

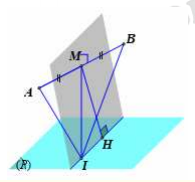
Cách 2: Tham khảo hình bên

Ta có I thuộc giao tuyến mặt phẳng trung trực AB và $\left(P\right)\Rightarrow IM\ge MH$ 

$\Rightarrow R\ge HA\Rightarrow R_{min}=HA$ với H là hình chiếu của M trên giao tuyến $\Rightarrow R_{min}=\frac{\sqrt{462}}{6}$