Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng P qua B

* Hướng dẫn giải

Đáp án B

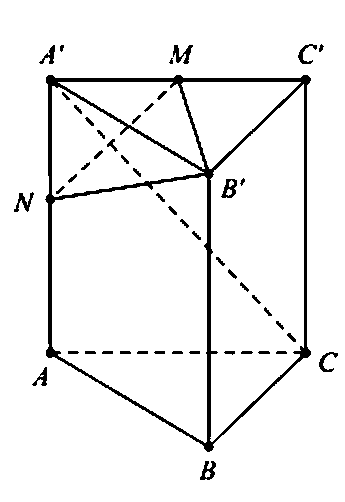Gọi M là trung điểm A’C’. Ta có $B\text{'}M\perp \left(ACC\text{'}A\text{'}\right)\Rightarrow B\text{'}M\perp A\text{'}C$.

Suy ra $M\in mp\left(P\right)$. Kẻ $MN\perp A\text{'}C(N\in AA\text{'})\Rightarrow N\in mp\left(P\right)$ 

Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN

Hai tam giac A’C’C và NA’M đồng dạng $\Rightarrow A\text{'}N=\frac{1}{2}A\text{'}M=\frac{a}{4}$ 

Thể tích tứ diện A'B'MN là $V_1=\frac{1}{3}A\text{'}N.S_{∆A\text{'}B\text{'}M}=\frac{a^3\sqrt{3}}{96}$ 

Thể tích lăng trụ là $V=AA\text{'}.S_{∆ABC}=\frac{a^3\sqrt{3}}{2}$. Vậy $\frac{V_1}{V_2}=\frac{1}{47}$.