Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 1 - Hình học 6
Tóm tắt bài
Đề bài
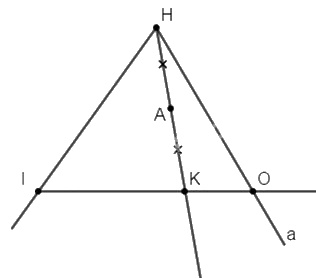
Bài 1. Vẽ ba điểm H, I, K không thẳng hàng. Vẽ hai tia HI và HK. Vẽ tia Ha cắt tia IK tại điểm O sao cho K nằm giữa I và O. Vẽ điểm A là trung điểm của đoạn thẳng HK.
Bài 2. Cho đoạn thẳng AB. Trên tia đối của tia AB lấy điếm M, trên tia đối củùa tia BA lấy điểm N sao cho BN = AM. Chứng tỏ rằng BM = AN.
Bài 3. Cho đoạn thẳng AB = 8cm. Gọi I là trung điểm của AB.
a) Tính IA, IB.
b) Trên A, B lấy hai điểm C và D sao cho \(AC = BD = 3cm\). Tính IC, ID.
c) Hỏi I có là trung điểm của CD không?
Hướng dẫn giải
Bài 1. Xem hình vẽ
Bài 2.

M thuộc tia đối của tia AB nên AM và AB là hai tia đối nhau.
Do đó A nằm giữa hai điểm M và B. Ta có \(MB = MA + AB.\)
Tương tự, ta có B nằm giữa hai điểm N và B nên \(NA = NB + AB\), mà
\(MA = NB =5 ⇒ MB = AN.\)
Bài 3.
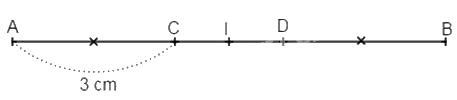
a) I là trung điếm của AB nên \(IA = IB =\dfrac {{AB} }{ 2} = \dfrac{8 }{ 2} = 4(cm)\)
b) C, I thuộc AB mà \(AC \( AC + CI = AI\) \(3 + CI = 4\) \(CI = 4 - 3 = 1\, (cm).\) Tương tự ta có D nằm giữa hai điểm B và I và ID = 1 (cm) c) Vì I là trung điểm của AB nên IA và IB là hai tia đối nhau C thuộc tia I, D thuộc IB nên IC và ID là hai tia đối nhau Do đó I nằm giữa hai điểm C và D (1) Lại có: \(CI = ID = 1\; (cm)\) (2) Từ (1) và (2) ta có I là trung điểm của CD
Copyright © 2021 HOCTAP247
