Bài 39 trang 71 SGK Toán 7 tập 1
Tóm tắt bài
Đề bài
Vẽ trên cùng một hệ trục toạ độ \(Oxy\) đồ thị của các hàm số:
a) \(y = x\); b) \(y = 3x\);
c) \(y = -2x\); d) \(y = -x\).
Hướng dẫn giải
Đồ thị hàm số \( y = ax + b\left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ.
Sau đó ta lấy x bất kỳ tìm y để tìm được tọa độ điểm thứ 2 gọi là điểm A mà đồ thị đó đi qua.
Vẽ đường thẳng đi qua điểm O và A ta được đồ thị cần tìm
Lời giải chi tiết
a) \(y = x\)
- Vẽ hệ trục tọa độ \(Oxy\)
- Cho \(x = 0\) được \(y = 0\) \(\Rightarrow O (0; 0)\) thuộc đồ thị hàm số \(y=x\).
- Cho \(x = 2\) được \(y = 2\) \(\Rightarrow A (2; 2)\) thuộc đồ thị hàm số \(y=x\).
Vậy đường thẳng \(OA\) là đồ thị của hàm số đã cho.
b) \(y = 3x\)
- Vẽ hệ trục tọa độ \(Oxy\)
- Cho \(x = 0\) được \(y = 0\) \(\Rightarrow O (0; 0)\) thuộc đồ thị hàm số \(y=3x\).
- Cho \(x = 1\) được \(y = 3\) \(\Rightarrow B (1; 3)\) thuộc đồ thị hàm số \(y=3x\).
Vậy đường thẳng \(OB\) là đồ thị của hàm số đã cho.
c) \(y = -2x\)
- Vẽ hệ trục tọa độ \(Oxy\)
- Cho \(x = 0\) được \(y = 0\). Điểm \(O (0; 0)\) thuộc đồ thị của hàm số \(y = -2x\).
- Cho \(x = -1\) được \(y = 2\). Điểm \(C (-1; 2)\) thuộc đồ thị của hàm số \(y = -2x\).
Vậy đường thẳng \(OC\) là đồ thị của hàm số đã cho.
d)
\(y = -x\)
- Vẽ hệ trục tọa độ \(Oxy\)
- Cho \(x = 0\) được \(y = -0\). Điểm \(O (0; 0)\) thuộc đồ thị của hàm số \(y = -2x\).
- Cho \(x = 1\) được \(y = -1\). Điểm \(D (1; -1)\) thuộc đồ thị của hàm số \(y = -x\).
Vậy đường thẳng \(OD\) là đồ thị của hàm số đã cho.
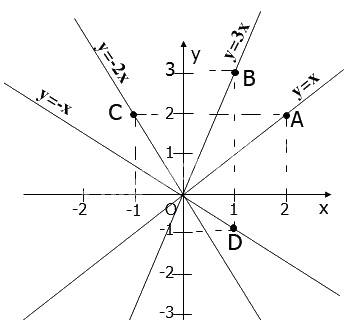
Ta có đồ thị như sau:
Copyright © 2021 HOCTAP247
