Đề kiểm tra 15 phút - Đề số 11 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC (AB < AC). Gọi M trung điểm của BC. Vẽ BH vuông góc với AM (H thuộc AM) và CK vuông góc với AM (K thuộc AM). Chứng minh rằng BH = CK.

Hướng dẫn giải

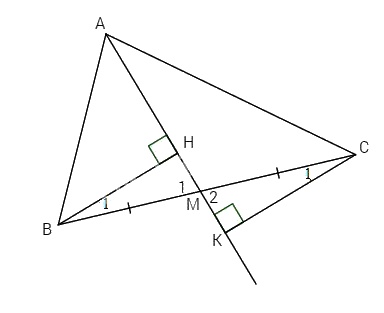
Ta có  \(BH \bot AM,\,CK \bot AM\) (giả thiết)

\( \Rightarrow BH//CK\) (hai đường thẳng phân biệt cùng vuông góc với đường thứ ba thì song song với nhau)

\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\) (cặp góc so le trong)

Xét \( \Delta BHM \) và \( \Delta CKM\) có:

+) \(\widehat {{M_1}} = \widehat {{M_2}}\)(đối đỉnh)

+) \(MB = MC\) (giả thiết);

+) \(\widehat {{B_1}} = \widehat {{C_1}}\) (chứng minh trên)

\(\Rightarrow \Delta BHM = \Delta CKM\) (g.c.g)

Do đó \(BH = CK\) (cạnh tương ứng).