Đề kiểm tra 15 phút - Đề số 15 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
Tóm tắt bài
Đề bài
Cho góc \(\widehat {xOy}\) khác góc bẹt, có Ot là tia phân giác. Qua điểm H thuộc tia Ot kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự ở A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh B, C, E thẳng hàng.
Hướng dẫn giải
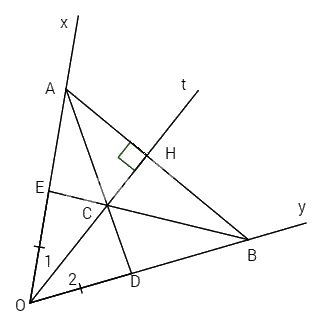
a) Xét \(\Delta OHA\) và \(\Delta OHB\) có
+) \(\widehat {{O_1}} = \widehat {{O_2}}\) (giả thiết);
+) OH cạnh chung; \(\widehat {OHA} = \widehat {OHB} = {90^o}\) (giả thiết)
Do đó \(\Delta OHA=\Delta OHB\) (g.c.g) \( \Rightarrow OA = OB.\)
b) Xét \(\Delta OCE \) và \( \Delta OCD\) có:
+) OC cạnh chung,
+) \(\widehat {{O_1}} = \widehat {{O_2}}\) (giả thiết),
+) OE = OD (giả thiết).
Do đó \(\Delta OCE = \Delta OCD\) (c.g.c)
\( \Rightarrow \widehat {OCE} = \widehat {OCD}\)(góc tương ứng).
Xét \(\Delta OCA \) và \( \Delta OCB\) có:
+) OC cạnh chung;
+) \(\widehat {{O_1}} = \widehat {{O_2}}\) (giả thiết);
+) OA = OB (chứng minh trên)
Vậy \(\Delta OCA = \Delta OCB\) (c.g.c)
\( \Rightarrow \widehat {OCA} = \widehat {OCB}\) (2 góc tương ứng).
Mà \(\widehat {OCA} + \widehat {OCD} = {180^o} \)
\(\Rightarrow \widehat {OCB} + \widehat {OCE} = {180^o}\)
Chứng tỏ B, C, E thẳng hàng.
Copyright © 2021 HOCTAP247
