Bài 88 trang 111 SGK Toán 8 tập 1

Đề bài

Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:

a) Hình chữ nhật?

b) Hình thoi?      

c) Hình vuông

Hướng dẫn giải

Áp dụng: - Tính chất đường trung bình của tam giác.

- Dấu hiêuj nhaạn biết: hình chữ nhật, hình thoi, hình vuông.

Lời giải chi tiết

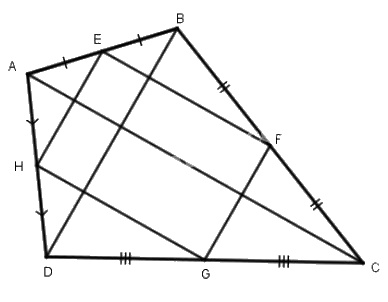
Ta có: EB = EA, FB = FC (gt)

Nên EF //AC, EF =  \({1 \over 2}\) AC (tính chất đường trung bình của tam giác)

HD = HA, GD = GC (gt)

Nên HG // AC, HG =  \({1 \over 2}\)AC (tính chất đường trung bình của tam giác)

Do đó EF //HG, EF = HG.

EB = EA, AH = HD (gt)

Nên EH //BD, EH =  \({1 \over 2}\) BD (tính chất đường trung bình của tam giác)

CF = FB, GD = GC (gt)

Nên FG // BD, FG =  \({1 \over 2}\)BD (tính chất đường trung bình của tam giác)

Do đó EH // FG, EH = FG

Vậy EFGH là hình bình hành.

a) Hình bình hành EFGH là hình chữ nhật ⇔EH  ⊥ EF

   ⇔ AC ⊥ BD (vì EH // CD. EF // AC)

Điều kiện phải tìm: các đường chéo AC và BD vuông góc với nhau.

b) Hình bình hành EFGH là hình thoi ⇔ EF = EH

  ⇔AC = BD (vì  \(EF = {1 \over 2}AC, EH = {1 \over 2}BD)\)

Điều kiện phải tìm: các đường chéo AC và BD bằng nhau.

c) Hình bình hành EFGH là hình vuông.

EFGH là hình vuông đồng thời là hình thoi

=> AC ⊥ BD và AC = BD

Điều kiện phải tìm: các đường chéo AC, BD bằng nhau và vuông góc với nhau.