Lý thuyết chuẩn nhất về hình chóp đều - Toán học 8

Trong bài viết này gửi đến bạn những kiến thức lý thuyết về hình chóp đều là gì, thể tích hình chóp đều, tính chất hình chóp đều và chỉ bạn cách vẽ hình chóp đều chuẩn nhất.

I) Hình chóp đều là gì?

1) Khái niệm

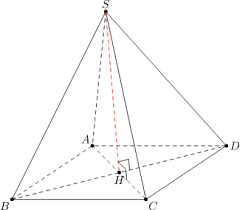
Hình chóp mà có các mặt bên là tam giác cân, có đáy là hình đa giác đều thì được gọi là hình chóp đều.

2) Tính chất

Chân đường cao của hình chóp đều là tâm của đáy.

II) Thể tích hình chóp đều

1) Tính thể tích hình chóp đều

\(V = \dfrac {1}{3}S.h\)

2) Tính thể tích hình chóp cụt đều

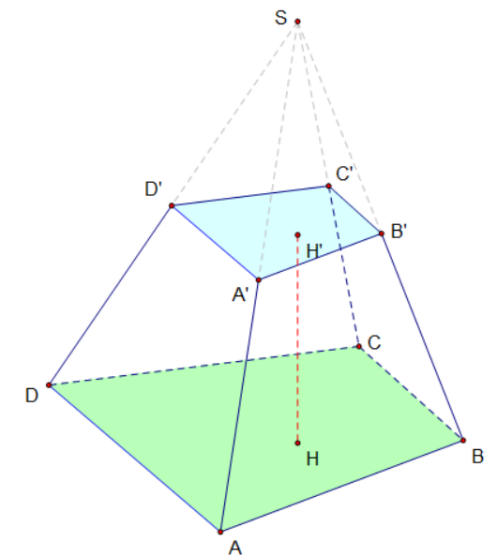
\(V = \dfrac {1}{3}h.(B+B' + \sqrt{B.B'})\)

III) Hướng dẫn cách vẽ hình chóp đều

Tùy vào từng yêu cầu, đề bài mà ta có đáy của hình chóp là tam giác đều hay hình vuông.

- Với hình chóp tam giác đều:

• Đáy là tam giác đều
• Cạnh bên bằng nhau
• Mặt bên là tam giác cân bằng nhau
• Chân đường cao trùng với tâm đáy
• Góc tạo bởi cạnh bên (mặt đáy) và mặt đáy bằng nhau

- Với hình chóp tứ giác đều

• Có đáy là hình vuông
• Cạnh bên bằng nhau
• Mặt bên là tam giác cân bằng nhau
• Chân đường cao trùng với tâm mặt đáy
• Góc tạo bởi cạnh bên (hoặc mặt bên) và mặt đáy bằng nhau

IV) Luyện tập

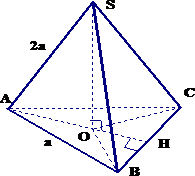
Bài 1: Hình chóp đều SABC, đáy bằng a, cạnh bên bằng 2a. Kẻ đường cao SO xuống mặt phẳng đáy ABC. Hãy:

a) CMR: O là tâm của tam giác đều ABC

b) \(V_{SABC}\)

 

Hướng dẫn:

b) \(V = \dfrac {a^3\sqrt{11}}{12}\)

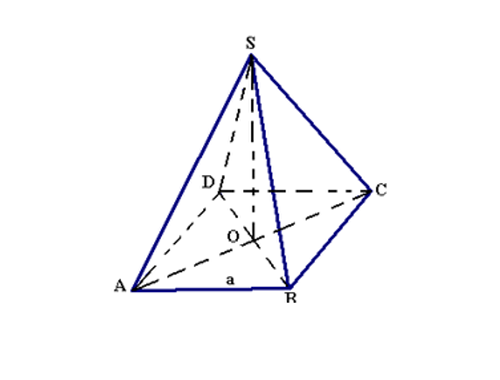
Bài 2: Cho hình chóp tứ giác đều S.ABCD, các cạnh đều bằng a. Hãy

a) CMR: S.ABCD là chóp tứ giác đều

b) \(V_{SABCD}=?\)

Hướng dẫn:

b) \(V_{SABCD}= \dfrac{a^3\sqrt{2}}{6}\)

Trên đây là bài viết mà đã tổng hợp được về hình chóp đều là gì, tính chất của hình chóp đều, công thức tính thể tích của hình chóp đều và cách vẽ hình chóp đều. Đừng quên để lại comment lời giải và ý kiến thắc mắc của các bạn ở phía dưới, chúc các bạn học tập tốt