Bài 4 trang 42 SGK Đại số 10

Đề bài

Vẽ đồ thị hàm số.

a) 

\(y = \left\{ \matrix{
2x\text{ với }x \ge 0 \hfill \cr
- {1 \over 2}x\text{ với }x < 0 \hfill \cr} \right.\)

 b) 

\(y = \left\{ \matrix{
x + 1\text{ với }x \ge 1 \hfill \cr
- 2x + 4\text{ với }x < 1 \hfill \cr} \right.\)

Hướng dẫn giải

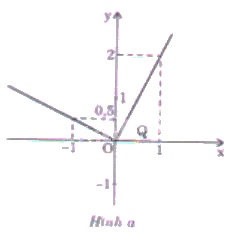
a) +) Vẽ đường thẳng \(y=2x\) với \(x\ge0\)

Đường thẳng \(y=2x\) đi qua hai điểm \(A(0;0)\) và \(B(1;2)\). Trên đường thẳng này ta giữ nguyên phần đường thẳng ứng với \(x\ge 0\) còn xóa bỏ phần còn lại ta được đồ thị của đường thẳng \(y=2x\) với \(x\ge0\).

     +) Vẽ đường thẳng \(y=- {1 \over 2}x\) với \(x

Đường thẳng \(y=- {1 \over 2}x\) đi qua hai điểm \(A(0;0)\) và \(B(-1;{1 \over 2})\). Trên đường thẳng này ta giữ nguyên phần ứng với \(x

Đồ thị của hàm số đã cho là hai đồ thị của hai hàm số \(y=2x\) với \(x\ge0\) và \(y=- {1 \over 2}x\) với \(x

b)

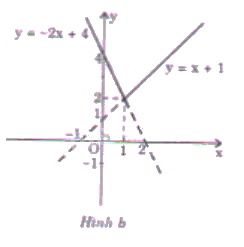
- Vẽ đường thẳng y = x + 1 đi qua điểm A (1; 2) và B (2; 3). Trên đường thẳng này, ta giữ phần đường thẳng khi x ≥ 1.

- Vẽ đường thẳng y = -2x + 4 đi qua điểm A (1; 2) và B' (0; 4). Trên đường thẳng này, ta giữ phần đường thẳng khi x

Khi đó đồ thị của hàm số đã cho là hai đồ thị \(y=x + 1\) với  \(x \ge 1\) (phần nét liền) và \(y= - 2x + 4\) với  \(x