Bài 7 trang 58 SGK Vật lí 10

Đề bài

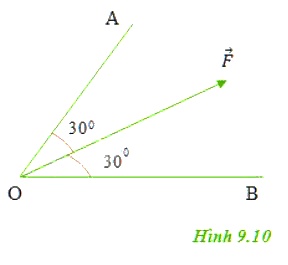
Phân tích lực \(\vec{F}\)  thành hai lực \(\vec{F_{1}}, \vec{F_{2}}\)  theo hai phương OA và OB (Hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần.

A. F₁ = F₂ = F;                     B.  F₁ = F₂ = \(\frac{1}{2}\)F

C. F₁ = F₂ = 1,15F               D.  F₁ = F₂ = 0,58F.

Hướng dẫn giải

Áp dụng quy tắc hình bình hành và sử dụng kiến thức hình học.

Lời giải chi tiết

Đáp án D

Áp dụng quy tắc hình bình hành: từ điểm ngọn của vecto \(\vec{F}\) lần lượt vẽ các đoạn thẳng song song với OA và OB ta được \({\overrightarrow F _1}\) trên OA và \({\overrightarrow F _2}\) trên OB sao cho: \(\overrightarrow F  = {\overrightarrow F _1} + {\overrightarrow F _2}\)

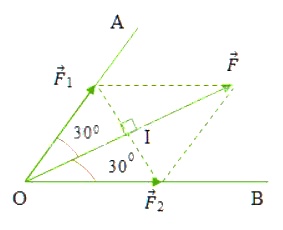
Ta có: hình bình hành OF₁FF₂ có đường chéo OF là đường phân giác của góc O nên OF₁FF₂ là hình thoi.

Tam giác F₁OI vuông tại I có:

\(\eqalign{
& \cos 30 = {{OI} \over {{\rm{O}}{{\rm{F}}_1}}} \cr& \Rightarrow {\rm{O}}{{\rm{F}}_1} = {{OI} \over {\cos 30}} = {{{{OF} \over 2}} \over {\cos 30}} = 0,58.{\rm{OF}} \cr
& \Rightarrow {F_1} = {F_2} = 0,58F \cr} \)