Bài 2 trang 19 SGK Hình học 11
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A(2;0)\) và đường thẳng \(d\) có phương trình \(x+y-2=0\). Tìm ảnh của \(A\) và \(d\) qua phép quay tâm \(O\) góc \( 90^{\circ}\)
Hướng dẫn giải
Sử dụng hình vẽ trên mặt phẳng tọa độ Oxy và dựa vào định nghĩa phép quay.
Lời giải chi tiết
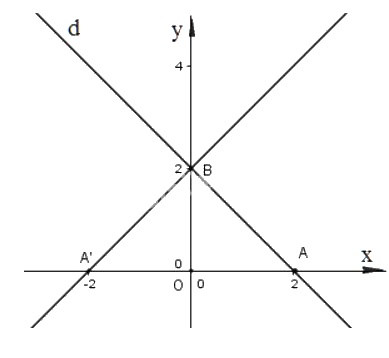
Lấy \(A(2;0), B(0;2)\) thuộc \(d\)
Ta có \({Q_{\left( {O;{{90}^0}} \right)}}\left( A \right) = B;\,\,{Q_{\left( {O;{{90}^0}} \right)}}\left( B \right) = A'\).
Do đó ảnh của \(d\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) là đường thẳng \(BA'\) có phương trình \(\frac{x}{{ - 2}} + \frac{y}{2} = 1 \Leftrightarrow x - y + 2 = 0\)
Copyright © 2021 HOCTAP247
