Các phép dời hình lớp 11
Tóm tắt bài
Các phép dời hình lớp 11
Hôm nay sẽ chia sẻ với các bạn về lý thuyết về phép dời hình lớp 11!
I. Phép tịnh tiến?
1. Định nghĩa
Được định nghĩa là cách dời một hình ban đầu sao cho mọi thông số đều được bảo toàn và khoảng cách giữa hai điểm bất kỳ của hình không đổi.
Nếu một phép dời hình áp dụng bất kỳ cho một điểm F và khiến cho các điểm M và N lần lượt trở thành các điểm M' và N' sao cho bảo toàn điều kiện MN=M'N'.
Nhận xét:
1) Các phép khác trong mặt phẳng tọa độ như phép đồng nhất, vị tự hay tịnh tiến... đều thuộc lý thuyết của phép dời hình với các đặc điểm khác nhau.
2) Đặc điểm của phép biến hình được tạo nên bởi cách tạo ra hai phép dời hình liên tiếp.
2. Tính chất
- Định lý 1: Khoảng cách giữa ba điểm bất kỳ sau khi áp dụng phép dời hình sẽ được bảo toàn hoàn toàn. Bên cạnh đó sẽ duy trì các tính chất cũ của đường thẳng cũng như ba điểm ban đầu.
- Định lý 2: Với trường hợp đặc biệt của ba điểm thẳng hàng thì việc áp dụng phép tịnh tiến sẽ không gây ra những thay đổi về mặt thứ tự của các điểm đó.
3. Hệ quả
- Đường thẳng ban đầu sau khi áp dụng phép tịnh tiến sẽ cho ra một đường thẳng mới song song với đường thẳng cũ hoặc đặc biệt là trùng nhau với đường thẳng ban đầu.
- Tương tự đoạn thẳng mới được tạo ra cũng bằng hoàn toàn so với đoạn thẳng ban đầu.
- Tam giác cũng tương tự so với đường thẳng, bằng với tam giác cũ.
- Tương tự với trường hợp là đường tròn, không có sự thay đổi, bằng với đường tròn ban đầu.
- Là góc cũng tương tự như những trường hợp trên. Góc mới được tạo ra hoàn toàn trùng khớp với góc ban đầu khi áp dụng phép dời hình.
Phép đồng dạng có phải phép dời hình không? Câu trả lời là có và chỉ đúng với trường hợp hai tam giác đồng dạng bằng nhau hoàn toàn. Năm chắc được tính chất của phép dời hình ta hoàn toàn có thể áp dụng để chứng minh hai tam giác có liên quan bằng nhau.
Giải bài tập phép tịnh tiến và phép dời hình
Chú ý:
1) Trong trường hợp là tam giác thì ta có thể chứng minh điều biến các điểm đối xứng trọng tâm, trực tâm và các điểm đặc biệt của tam giác thành trọng tâm, trực tâm và tất cả các điểm đặc biệt khác của tam giác đối xứng.
2) Đối với một đa giác gồm có n cạnh ta sẽ biến nó thành đa giới n qua hình thức dời hình, đỉnh mới đối xứng với đỉnh cũ và cạnh mới đối xứng với cạnh cũ.
IV. Bài tập phép dời hình lớp 11
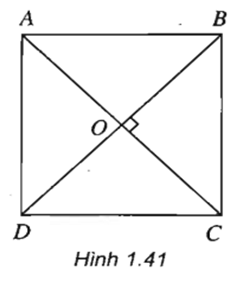
Bài 1: Hình vuông ABCD ta lấy giao điểm của AC và BD tại O. Tìm ảnh cho các điểm A, B, O bằng cách áp dụng phép dời hình bằng cách thực hiện phương pháp quay một góc 90 độ qua trục đối xứng BD.
Lời giải
- Phản chiếu của ba điểm A, B, O lần lượt qua phép quay 90 độ là các điểm D, A, O.
- Hình phản chiếu của ba điểm D, A, O lần lượt là qua phép đối xứng trục BD là D, C, O.
Bài 2: Chứng minh tính đúng đắn của tính chất số 1.
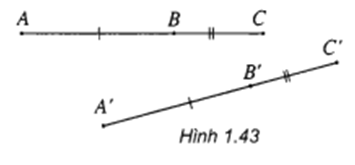
Hướng dẫn chung: Áp dụng tính xác thực của nội dung của tính chất khi điểm B nằm giữa hai điểm A và C khi và chỉ khi AB + BC = AC (h.1.43). Đâu không phải phép dời hình.
Lời giải
Áp dụng định nghĩa: phép dời hình là phép biến hình bảo toàn khoảng cảnh giữa hai điểm bất kỳ
Nên ảnh của 3 điểm A, B, C qua phép dời hình F là 3 điểm A', B', C'
Bài tập tự luyện:
Bài 1: Cho A(3;4). Tìm tọa độ \(A'=Q_{(o;90^0)}(A)\)
Bài 2: Cho A(2;0), d: x + y - 2 = 0. Xác định hình ảnh phản diện ứng với điểm A đó qua trục chiếu d với phép dời hình có góc quay 90 độ
Bài 3: Một hình vuông ABCD cho trước có một tâm I(1;2). Biết đỉnh A(4;5). Tìm tọa độ B; C; D
Bài 4: Cho d: x + y + 1 = 0; I(1;-2). Phép dời hình \(Q_{(o;90^0)}(d)=d'\). Xác định phương trình của d’.
Bài 5: Trong mặt phẳng Oxy cho ∆ : 2x -y +1= 0 . Tìm ảnh của đường thẳng ∆ qua :
a) Phép đối xứng tâm I(1; -2)
b) Phép dời hinhf với góc \(Q_{(o;90^0)}\)
Bài 6: Trong mặt phẳng tọa độ Oxy. Tìm phép dời hình Q biến A(-1;5) thành B(5;1)
Bài 7: ∆ABC đều có tâm O và phép dời hình \(Q_{(o;120^0)}\)
a) Xác định ảnh của các đỉnh A, B, C qua phép dời hình \(Q_{(o;120^0)}\)
b) Xác định ảnh của ∆ABC qua phép dời hình \(Q_{(o;120^0)}\).
Hy vọng với những kiến thức bổ ích mà muốn chia sẻ về lý thuyết cần thiết để đạt được điểm cao tại các đề kiểm tra phép dời hình và học tốt hơn môn Toán học!
Copyright © 2021 HOCTAP247