Bài 3 trang 33 SGK Hình học 11
Tóm tắt bài
Đề bài
Trong mặt phẳng \(Oxy\) cho điểm \(I (1;1)\) và đường trong tâm \(I\) bán kính \(2\). Viết phương trình của đường trong là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm \(O\), góc \( 45^{\circ}\) và phép vị tự tâm \(O\), tỉ số \( \sqrt{2}\).
Hướng dẫn giải
Phép quay tâm O, góc quay \(45^0\) biến đường tròn tâm I bán kính R thành đường tròn tâm I' bán kính R, với \(I' = {Q_{\left( {I;{{45}^0}} \right)}}\left( I \right)\).
Phép vị tự tâm O, tỉ số \(\sqrt{2}\) biến đường tròn tâm I', bán kính R thành đường tròn tâm I''; bán kính R', với \(I'' = {V_{\left( {O;\sqrt 2 } \right)}}\left( I \right);\,\,R' = \sqrt 2 R\).
Lời giải chi tiết
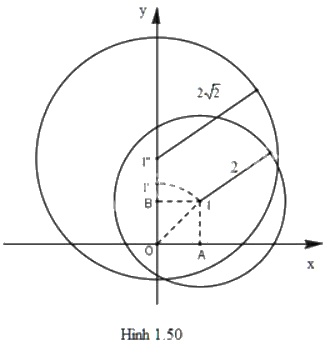
Gọi \(I'(x';y') = {Q_{\left( {I;{{45}^0}} \right)}}\left( I \right)\) ta có: \(\left\{ \begin{array}{l}x' = 1.\cos 45 - 1.\sin 45 = 0\\y' = 1.\sin 45 + 1.\cos 45 = \sqrt 2 \end{array} \right. \Rightarrow I'\left( {0;\sqrt 2 } \right)\)
Do đó phép quay tâm O, góc quay \(45^0\) biến đường tròn tâm I bán kính R thành đường tròn tâm \(I'\left( {0;\sqrt 2 } \right)\) bán kính \(R=2\).
Gọi \(I''\left( {x'';y''} \right) = {V_{\left( {O;\sqrt 2 } \right)}}\left( I \right)\) ta có:
\(\overrightarrow {OI''} = 2\overrightarrow {OI'} \Leftrightarrow \left\{ \begin{array}{l}x'' = 2.0 = 0\\y'' = 2.\sqrt 2 \end{array} \right. \Rightarrow I''\left( {0;2\sqrt 2 } \right)\)
Do đó phép vị tự tâm O, tỉ số \(\sqrt{2}\) biến đường tròn tâm I', bán kính R thành đường tròn tâm \(I''\left( {0;2\sqrt 2 } \right)\); bán kính \(R' = \sqrt 2 R = 2\sqrt 2 \).
Vậy phương trình đường trỏn tâm I'', bán kính R' là \({x^2} - {\left( {y - 2\sqrt 2 } \right)^2} = 8\).
Copyright © 2021 HOCTAP247
