Bài giảng đường thẳng vuông góc với mặt phẳng

Bài giảng đường thẳng vuông góc với mặt phẳng

Bài viết dưới đây  sẽ giúp các bạn làm sáng tỏ nội dung lý thuyết về đường thẳng vuông góc với mặt phẳng lớp 11!

I. Lý thuyết?

1. Định nghĩa

    

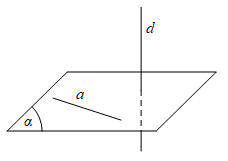
Đường vuông với mặt phẳng khi đường thẳng d đó vuông góc với bất cứ đường thẳng nào thuộc mặt phẳng ban đầu.

Kí hiệu thể hiện đường vuông với mặt phẳng như sau: d ⊥ (α).

2. Điều kiện để đường thẳng vuông góc với mặt phẳng

Định lí: Và nếu ta chứng minh được một đường thẳng bất kỳ cùng vuông góc đồng thời với hai đường thẳng đó thì cũng sẽ vuông góc với mặt phẳng chứa hai đường thẳng đó.

Hệ quả: Xét một tam giác bất kỳ nếu một đường thẳng bất kỳ trong không gian đã vuông góc với hai cạnh của tam giác thì chắc chắn sẽ vuông góc với cạnh còn lại của tam giác đó.

3. Tính chất

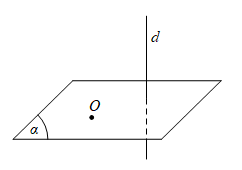
Tính chất 1: Chỉ tồn tại duy nhất một điểm mà qua đó tìm được một mặt phẳng duy nhất sao cho qua nó và vuông góc với một đường thẳng cho trước.

    

Mặt phẳng tương đương trung trực của một đường thẳng d: Khi mặt phẳng đó đi qua trung điểm và vuông góc với đường thẳng tại đúng trung điểm xác định đó.

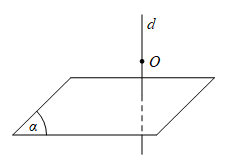
Tính chất 2: Qua một điểm xác định cho trước ta cũng chỉ tìm được một đường thẳng duy nhất đi qua nó và vuông góc với một mặt phẳng xác định ban đầu.

    

Giải bài tập đường thẳng vuông góc với mặt phẳng

4. Mối liên hệ về tính song song và vuông góc

Tính chất 1:

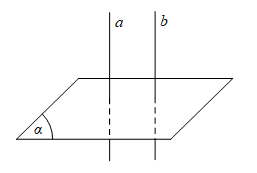
- Xét một mặt phẳng và hai đường thẳng song song bất kỳ, khi ta chứng minh được một đường thẳng này vuông góc với mặt phẳng ban đầu thì hiển nhiên suy ra được mặt phẳng cũng sẽ vuông góc với đường thẳng còn lại.

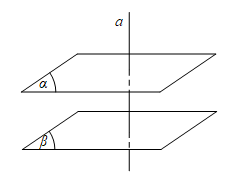
- Định lý đúng với điều ngược lại, hai đường thẳng được chứng minh là song song khi chúng cùng vuông góc với một mặt phẳng chung.

    

Tính chất 2:

- Đối với hai mặt phẳng song song cũng tương tự như hai đường thẳng song song, khi ta chứng minh được một mặt phẳng này vuông góc với một đường thẳng này thì cũng suy ra được mặt phẳng còn lại cũng vuông góc với đường thẳng còn lại.

    

Tính chất 3:

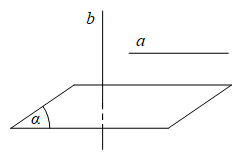
- Với một đường thẳng và một mặt phẳng bất kỳ. Nếu đường và mặt song song với nhau thfi khi đường thẳng vuông góc với mặt phẳng thì suy ra nó sẽ vuông góc với đường thẳng còn lại, nó hoàn toàn đúng với điều còn lại.

- Xét một mặt phẳng và một đường thẳng bất kỳ (biết rằng đường thẳng đó không nằm trong mặt phẳng) nên nếu đường thẳng và mặt phẳng cùng vuông góc với mọt đường thẳng thứ hai thì theo tính chất suy ra đường thẳng thứ nhất vuong góc với mặt phẳng.

    

II. Dạng bài tập đường thẳng vuông góc với mặt phẳng

Để chứng minh đường thẳng a vuông góc với mặt phẳng (P) ta thường sử dụng các phương pháp sau:

1). Muốn chứng minh đường thẳng a vuông góc với mặt phẳng (P). Ta phi chứng minh đường thẳng a vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng (P).

\(\begin{align} \begin{cases} a\bot b \& a\bot c \\ b\cap c\# I \\ b;c\cap (P) \end{cases}\end{align}\)\(\Rightarrow a\bot (P)\).

2). Hai mặt phẳng (Q) và (R) có giao tuyến a cùng vuông góc với mặt phẳng (P), thì a vuông góc với (P).

\(\begin{align} \begin{cases} (Q)\bot(P) \\ (R)\bot (P) \\ (Q)\cap(R)=a \end{cases}\end{align}\)\(\Rightarrow a\bot (P)\).

3). Hai mặt phẳng (P) và (Q) vuông góc với nhau theo giao tuyến b. Một đường thẳng a thuộc mặt phẳng (Q) vuông góc với b, thì a vuông góc với mặt phẳng (P).

\(\begin{align} \begin{cases} (P)\bot(Q) \\ (P)\cap (Q)=b \\ a\cap (Q)\\ a\bot b \end{cases}\end{align}\)\(\Rightarrow a\bot (P)\)

4). Chứng minh đường thẳng b vuông góc với mặt phẳng (P) , đường thẳng a song song với b ,suy ra a vuông góc với (P).

\(\begin{align} \begin{cases} a//b \\ b\bot (P) \end{cases}\end{align}\)\(\Rightarrow a\bot (P)\)

5). Chứng minh đường thẳng a song song với mặt phẳng (Q), mặt phẳng (P) song song với (Q), nên a vuông góc với (P).

\(\begin{align} \begin{cases} a\bot (Q) \\ (Q)//(P) \end{cases}\end{align}\)\(\Rightarrow a\bot (P)\)

Hai trụ cột để giải toán của dạng này:

- Muốn chứng minh đường thẳng d vuông góc với mặt phẳng (P), ta phi chứng minh đường thẳng d vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng (P).

- Khi đường thẳng d vuông góc với mặt phẳng (P) thì đường thẳng d vuông góc với mọi đường thuộc mặt phẳng (P).

III. Bài tập vận dụng

Bài 1: Cho tứ diện đều ABCD. Chứng minh các cặp cạnh đối diện của tứ diện này vuông góc với nhau từng đôi một.

Lời giải:

Giả sử cần chứng minh \(AB\bot CD\).

Gọi I là trung điểm của cạnh AB. Ta có: \(\left\{ \begin{array}{l}CI\bot AB\\DI\bot AB\end{array} \right.\Rightarrow AB\bot \left( CID \right)\).

Do đó \(AB\bot CD\) vì CD nằm trong mặt phẳng (CID).

Bằng lập luận tương tự ta chứng minh được \(BC\bot AD\) và \(AC\bot BD\).

Bài 2: Cho tứ diện OABC có ba cạnh OA,OB,OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mặt phẳng (ABC) tại H. Chứng minh:

    a) \(OA\bot BC,OB\bot CA\) và \(OC\bot AB\).

    b) H là trực tâm của tam giác ABC.

    c) \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}\).

Lời giải:

    a) Ta có \(\left\{ \begin{array}{l}OA\bot OB\\OA\bot OC\end{array} \right.\Rightarrow OA\bot \left( OBC \right)\Rightarrow OA\bot BC\).

    Tương tự ta chứng minh \(OB\bot \left( OCA \right)\Rightarrow OB\bot CA\).

                 \(OC\bot \left( OAB \right)\Rightarrow OC\bot AB\).

    b) Vì \(OH\bot \left( ABC \right)\) nên \(OH\bot BC\) và \(OA\bot BC\).

                \(\Rightarrow BC\bot \left( OAH \right)\Rightarrow BC\bot AH\).        (1)

    Chứng minh tương tự ta có \(AC\bot \left( OBH \right)\Rightarrow AC\bot BH\).        (2)

    Từ (1) và (2) suy ra H là trực tâm của tam giác ABC.

    c) Gọi K là giao điểm của AH và BC. Trong tam giác AOK vuông tại O, ta có OH đường cao.

    Dựa vào hệ thức lượng trong tam giác vuông của hình học phẳng ta có:

\(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{K}^{2}}}\)        (1)

    Vì BC vuông góc với mặt phẳng \(\left( OAH \right)\) nên \(BC\bot OK\). Do đó trong tam giác OBC vuông tại O với đường cao OK, ta có:

\(\frac{1}{O{{K}^{2}}}=\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}\)        (2)

Từ (1) và (2) suy ra \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}\).

Với những gì mà đã giúp các bạn khái quát nội dung về đường thẳng vuông góc mặt phẳng trên đây, hy vọng sẽ giúp các bạn đạt kết quả cao trong học tập!