Bài giảng thuyết electron định luật bảo toàn điện tích
Tóm tắt bài
Bài giảng thuyết electron định luật bảo toàn điện tích
Bài viết dưới đây sẽ giúp các bạn làm sáng tỏ nội dung lý thuyết về Lý 11 thuyết electron định luật bảo toàn điện tích!

I. Thuyết Electron
1. Nội dung lý thuyết:
- Trong hóa học và vật lý học, thuyết nguyên tử là một lý thuyết khoa học về bản chất của vật chất, cho rằng vật chất bao gồm các đơn vị rời rạc được gọi là các nguyên tử. Nó bắt đầu như là một khái niệm triết học trong Hy Lạp cổ đại và đi vào xu thế chủ đạo trong những năm đầu thế kỷ 19 khi những khám phá trong lĩnh vực hóa học cho thấy rằng vật chất thực sự hoạt động như thể nó được tạo thành từ các nguyên tử.
- Các nguyên tử từ xuất phát từ tính từ atomos trong tiếng Hy Lạp cổ đại, có nghĩa là "không thể chia cắt được". Các nhà hóa học thế kỷ 19 bắt đầu sử dụng thuật ngữ này liên hệ với số lượng ngày càng tăng của các yếu tố hóa học không thể rút gọn. Trong khi dường như thích hợp, khoảng đầu thế kỷ 20, thông qua các thí nghiệm khác nhau với điện từ, phóng xạ, các nhà vật lý đã phát hiện ra rằng cái gọi là "nguyên tử không thể chia cắt được" thực sự là một tập đoàn các hạt dưới nguyên tử khác nhau (chủ yếu là electron, proton và neutron) có thể tồn tại độc lập với nhau.
- Trong thực tế, trong môi trường khắc nghiệt nhất định, chẳng hạn như ở các ngôi sao neutron, nhiệt độ và áp suất cực cao ngăn cản không cho các nguyên tử tồn tại. Kể từ khi các nguyên tử được tìm thấy có thể phân chia được, các nhà vật lý sau này phát minh ra thuật ngữ "hạt cơ bản" để thay cho cụm từ "không thể chia cắt được", mặc dù không thể phá hủy, các bộ phận của một nguyên tử. Các lĩnh vực khoa học mà nghiên cứu các hạt dưới nguyên tử là vật lý hạt, và chính trong lĩnh vực này mà các nhà vật lý hy vọng sẽ khám phá ra bản chất cơ bản thực sự của vấn đề.
2. Mẫu hành tinh nguyên tử Rutherford
- Năm 1910, nhà vật lý người New Zealand Ernest Rutherford cho rằng các điện tích dương của nguyên tử đã được tìm thấy chủ yếu ở trung tâm của nó, trong hạt nhân và các electron (e-) xoay xung quanh nó.
- Rutherford cho thấy điều này khi ông sử dụng một nguồn bức xạ alpha (từ helium) để bắn vào các tấm vàng rất mỏng, được bao bọc bởi một chụp đèn kẽm sunfua tạo ra ánh sáng nhìn thấy được khi bị chiếu xạ tia alpha. Thí nghiệm này được gọi là thí nghiệm Geiger-Marsden hoặc thí nghiệm lá vàng.
- Đến giai đoạn này, các yếu tố chính của nguyên tử là rõ ràng, cộng với việc khám phá ra rằng các nguyên tử của một nguyên tố có thể xảy ra trong các đồng vị. Đồng vị khác nhau về số lượng các nơtron có trong hạt nhân. Mặc dù mô hình này đã được hiểu rõ, vật lý hiện đại đã phát triển hơn nữa, và những ý tưởng ngày nay không thể được thực hiện dễ dàng để hiểu được.
Trắc nghiệm thuyết electron định luật bảo toàn điện tích.
II. Định luật bảo toàn điện tích
1. Điện tích
- Điện tích tạo từ các hạt mang điện rất nhỏ, như một chất điểm, thì điện tích được gọi là điện tích điểm. Nếu điện tích điểm được sử dụng trong một thí nghiệm, có thể là thí nghiệm tưởng tượng trên lý thuyết, thì nó được gọi là điện tích thử.
- Điện tích còn được hiểu là "vật tích điện". Mọi vật trung hòa về điện khi cho hay nhận điện tử âm sẽ trở thành điện tích.
- Khi vật nhận electron vật sẽ tích điện âm:
Vật + e → Điện tích âm (-)
- Khi vật cho electron vật sẻ trở thành điện tích dươngː
Vật − e → Điện tích dương (+)
- Điện tích âm có ký hiệu − Q. Điện tích dương có ký hiệu + Q.
- Mọi điện tích đo bằng đơn vị Coulomb, ký hiệu C. Đơn vị Coulomb được định nghĩa như sau:
\({\displaystyle 1C=6,24\times 10^{18}}\) electron.
2. Tương tác điện
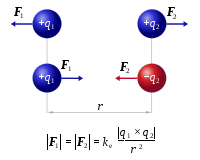
Tương tác giữa 2 điện tích điểm trong không gian
- Tương tác giữa hai điện tích
Khi hai điện tích tương tác với nhau, điện tích cùng loại đẩy nhau, điện tích khác loại hút nhau.
- Định luật Coulomb
Khi có 2 điện tích cách nhau một khoảng cách r thì lực tương tác của chúng tuân theo định luật Coulomb, gọi là lực Coulomb.
Định luật Coulomb phát biểu là:
Độ lớn lực tương tác giữa hai điện tích điểm tỷ lệ thuận với tích độ lớn của các điện tích và tỷ lệ nghịch với bình phương khoảng cách giữa chúng.
Công thức của định luật:
\({\displaystyle F=k{\frac {\left|q_{1}\right|\left|q_{2}\right|}{r^{2}}}}\)
Trong đó:
\({\displaystyle {\begin{aligned}k_{\mathrm {e} }&={\frac {1}{4\pi \varepsilon _{0}}}={\frac {c^{2}\ \mu _{0}}{4\pi }}=c^{2}\cdot 10^{-7}\ \mathrm {H} \cdot \mathrm {m} ^{-1}\\&=8,987.551.787\times 10^{9}\ \mathrm {N\cdot m^{2}/C^{2}} \end{aligned}}}\)
\({\displaystyle \epsilon _{0}\ }\) là hằng số điện, giá trị gần đúng thường dùng trong tính toán ở cấp phổ thông là \({\displaystyle 9\times 10^{9}\ \mathrm {N\cdot m^{2}/C^{2}} }\)
- Tương tác giữa điện tích và điện
Tương tác giữa điện tích đứng yên và điện có điện lực \({\displaystyle F_{E}}\) tạo ra dòng điện tích di chuyển thẳng hàng có điện trường E tuân theo định luật Ampere:
\({\displaystyle E={\frac {F_{E}}{Q}}}\)
Vì vậy \({\displaystyle F_{E}=QE}\)
- Tương tác giữa điện tích và từ
Tương tác giữa điện tích di chuyển và nam châm từ có từ lực \({\displaystyle F_{B}}\) tạo ra từ trường B vuông góc với điện trường E tuân theo định luật Lorentz:
\({\displaystyle F_{B}=QvB}\)
Vậy:
\({\displaystyle B={\frac {F_{B}}{Qv}}}\)
\({\displaystyle v={\frac {F_{B}}{QB}}}\)
- Tương tác giữa điện tích cùng với điện và từ
\({\displaystyle F_{EB}=F_{E}+F_{B}=QE\pm QvB=Q(E\pm vB)}\)
3 Lực điện tích
- Lực tĩnh điện: \({\displaystyle F_{Q}=K{\frac {|Q_{+}||Q_{-}|}{r^{2}}}}\)
- Lực động điện: \({\displaystyle F_{E}=QE}\)
- Lực động từ: \({\displaystyle F_{B}=\pm QvB}\)
- Lực điện từ: \({\displaystyle F_{EB}=Q(E\pm vB)}\)
III. Bài tập
Bài 1: q = -2,5.10-6 C, cho vào môi trường chịu tích điện là 5,5.10-6 C. Sau lần đầu nhiễm điện ta có hiện tượng xảy ra là:
A. nhận vào \(1,875.10^{13}\) electron.
B. nhường đi \(1,875.10^{13}\) electron.
C. nhường đi \(5.10^{13}\) electron.
D. nhận vào \(5.10^{13}\) electron.
Hướng dẫn:
Chọn C.
Thanh thép đang mang điện tích \(-2,5.10^{-6}\) để có điện tích \(5,5.10^{-6}\) thì thanh thép đã mất đi \(5,5.10^{-6} - (-2,5.10^{-6}) = 8.10^{-6}C.\)
⇒ Thanh thép đã nhường đi
\(n=\dfrac{|q|}{|e|}=\dfrac{8.10^{-6}}{1.6.20^{-19}}=5.10^{13} e\)
Bài 2: Nếu nguyên tử oxi bị mất hết electron nó mang điện tích
A. \(+1,6.10^{-19} C.\) B. \(–1,6.10^{-19} C.\)
C. \(+12,8.10^{-19} C.\) D. \(-12,8.10^{-19} C.\)
Hướng dẫn:
Chọn C.
Nguyên tử có 8 electron nên khi mất hết e thì nguyên tử mang điện tích dương với độ lớn:
\(|q| = n.|e| = 8.1,6.10^{-19} = 1,28.10^{-18} = C. +12,8.10^{-19} C.\)
Bài 3: Điện tích đặt lên A và B lần lượt là \(q_1 = -3,2.10^{-7}C, q_2 = 2,4.10^{-7}C\), khoảng giữa hai vật đo được tương ứng là 12 cm. Hai vật tiếp xúc nhẹ và cho trở về vị trí cũ khi ta lực tương tác là:
A. \(10^{-4}\) N B. \(10^{-3}\) N
C. 10N D. 1N
Hướng dẫn:
Chọn B.
Khi cho hai quả cầu tiếp xúc với nhau rồi tách chúng ra thì điện tích của mỗi quả cầu sau này là:
\(q_1'=q_2'=\dfrac{q_1+q_2}{2}=-0.4.10^{-7} C\)
Lực tương tác giữa chúng bây giờ là lực hút:
\(F=k.\dfrac{|q_1'.q_2'|}{r^2}=10^{-3}N\)
Với những gì mà đã giúp các bạn khái quát nội dung về giải bài thuyết electron định luật bảo toàn điện tích trên đây, hy vọng sẽ giúp các bạn đạt kết quả cao trong học tập!
Copyright © 2021 HOCTAP247