Giải bài 3 Trang 195 - Sách giáo khoa Vật lí 11
Tóm tắt bài
a) Sơ đồ tạo ảnh:
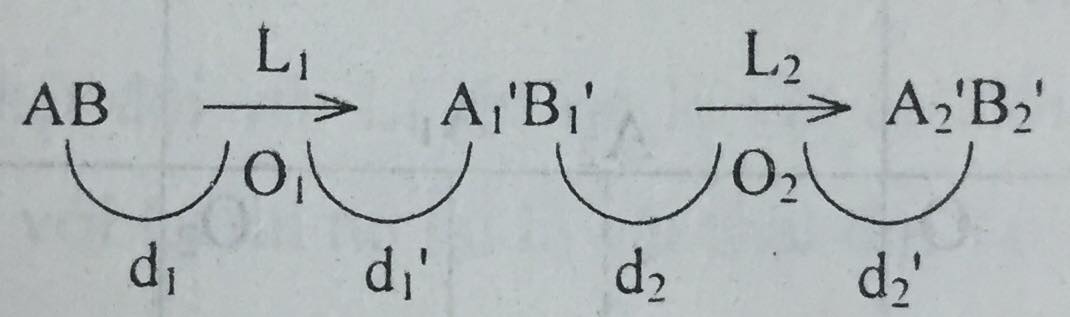
* Với thấu kính \(L_1\):
\(\dfrac{1}{d_1}+\dfrac{1}{d_1'}=\dfrac{1}{f_1} \Rightarrow \dfrac{1}{d_1'}=\dfrac{1}{f_1}-\dfrac{1}{d_1}=\dfrac{1}{20}-\dfrac{1}{20}=0 \Rightarrow d_1'=\infty\)
* Với thấu kính \(L_2\):
\(d_2=l-d_1'=\infty\)
Từ \(\dfrac{1}{d_2}+\dfrac{1}{d_2'}=\dfrac{1}{f_2} \Rightarrow d_2'=f_2=-10(cm).\)
Vẽ hình:
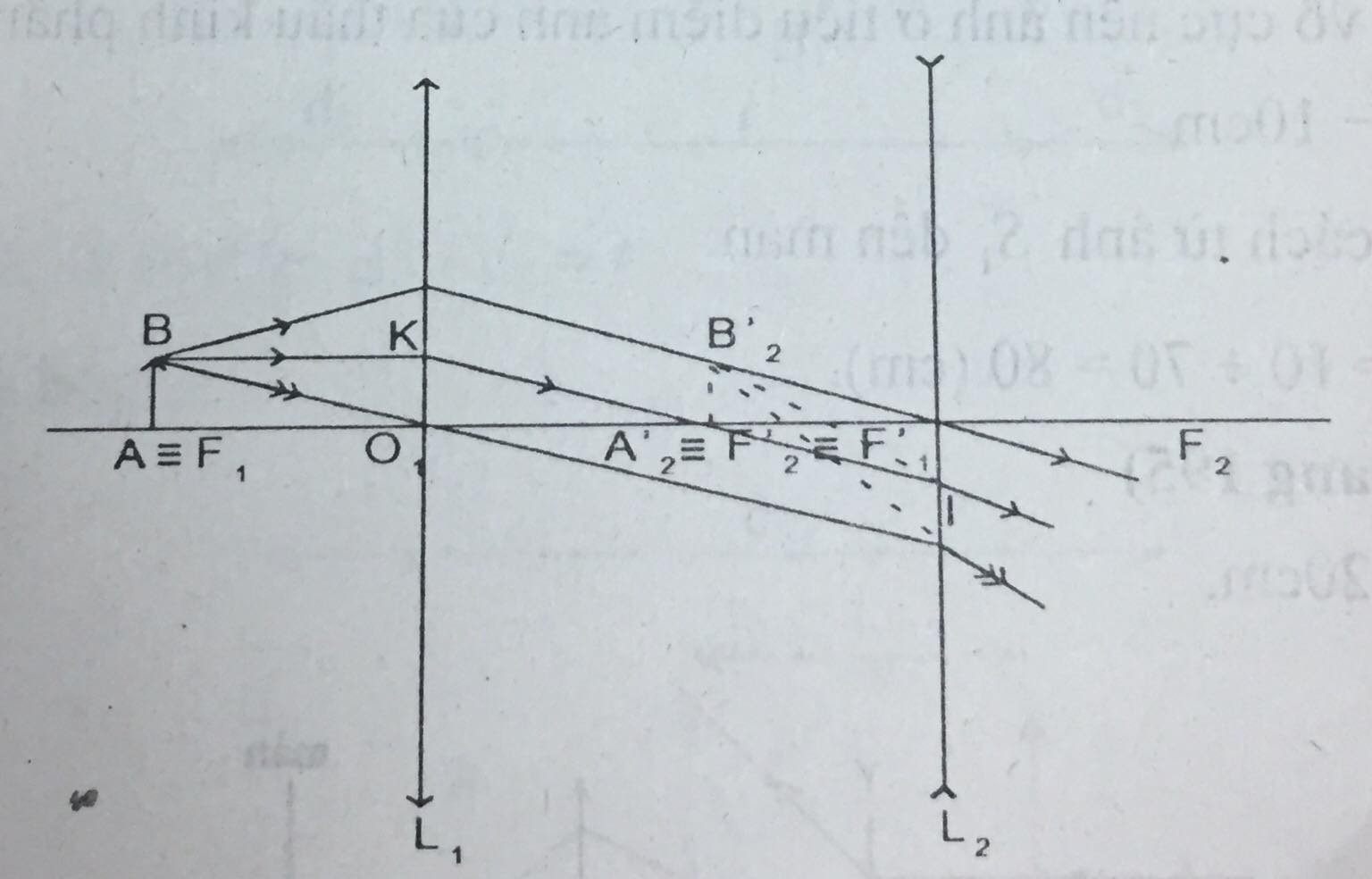
Xét hai tam giác đồng dạng \(O_1KF_2'\) và \(O_2IF_2'\):
\(\dfrac{O_2I}{O_1K}=\dfrac{O_2F_2'}{O_1F_1'}=\dfrac{f_2}{f_1} \Rightarrow \dfrac{\overline{A_2'B_2'}}{\overline{AB}}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\) độ phóng đại ảnh cuối cùng: \(k=\dfrac{1}{2}\)
b) Sơ đồ tạo ảnh:
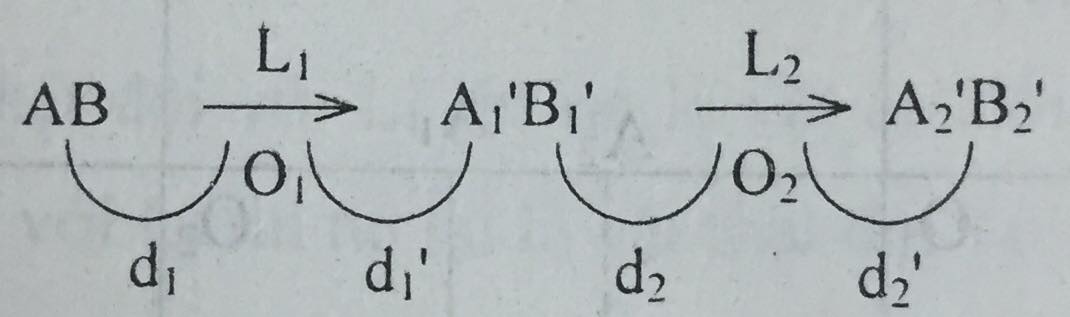
* Thấu kính \(L_1\):
\(d_1'=\dfrac{d_1f_1}{d_1-f_1}=\dfrac{20d_1}{d_1-20} \Rightarrow k=\dfrac{-d_1'}{d_1}=\dfrac{-20}{d_1-20}\)
\(d_2=l-d_1'=30-\dfrac{20d_1}{d_1-20}\) (1)
* Thấu kính \(L_2:\)
\(d_2'=\dfrac{d_2f_2}{d_2-f_2}=\dfrac{(-10)d_2}{d_2+10}\)
\(\Rightarrow k_2=\dfrac{-d_2'}{d_2}=\dfrac{\dfrac{10}{d_2+10}}{30-\dfrac{20d_1}{d_1-20}+10}=\dfrac{10(d_1-20)}{40(d_1-20)-20d_1} \Rightarrow k_2=\dfrac{10(d_1-20)}{20d_1-800}\)
Theo đề bài:
Trường hợp 1: \(k=2 \Rightarrow k_1k_2=2\)
\(\Rightarrow \dfrac{-20}{d_2-20}.\dfrac{10(d_2-20)}{20d_1-800}=2 \Leftrightarrow -10=2(d_1-40) \Leftrightarrow 2d_1=70 \Leftrightarrow d_1=35(cm).\)
Suy ra: \(d_1'=\dfrac{20.35}{35-20}=\dfrac{140}{3}(cm)\)
\(d_2=30-\dfrac{140}{3}=-\dfrac{50}{3}(cm)\)
\(d_2'=\dfrac{35.(-10)}{35+10}=-\dfrac{70}{9}<0\) (thỏa mãn)
Vậy, \(d_1'=35cm.\)
Trường hợp 2: \(k=-2 \Rightarrow k_1k_2=-2\)
\(\Rightarrow \dfrac{-20}{d_1-20}.\dfrac{10(d_1-20)}{20d_1-800}=-2 \Leftrightarrow -10=-2(d_1-40) \Leftrightarrow 2d_1=90 \Leftrightarrow d_1=45(cm).\)
Suy ra: \(d_1'=\dfrac{20.45}{20-45}=36(cm)\)
\(d_2=30-36=-6(cm)\)
\(d_1'=\dfrac{-6(-10)}{-6+10}=15(cm) >0\) (loại)
Vậy \(d_1=35cm.\)
Copyright © 2021 HOCTAP247
