Giải câu 6 trang 118- Sách giáo khoa Vật lí 9

   a) Khi \(d=36\)cm.

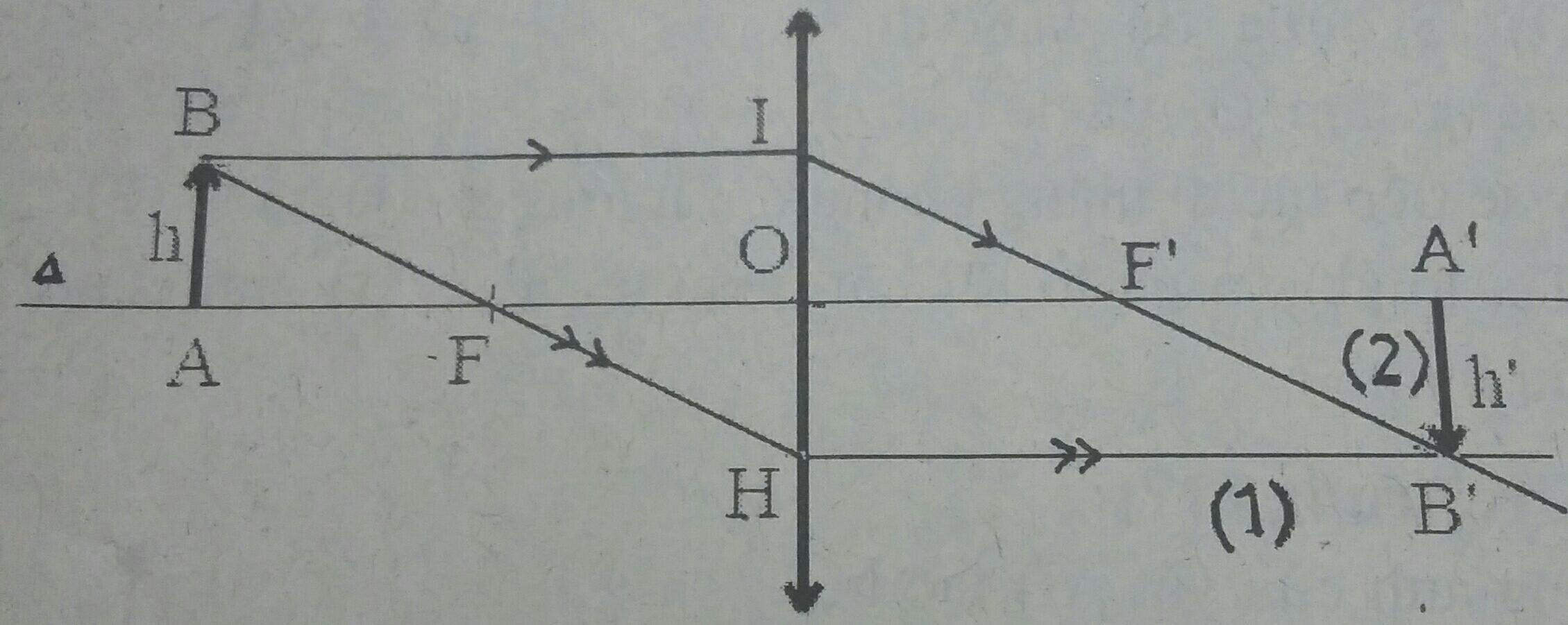
   Xét \(\Delta ABF \sim \Delta OHF\) , ta có công thức:

   \( \dfrac{OF}{AF}=\dfrac{OH}{AB}=\dfrac{h}{h'} \Rightarrow h' =\dfrac{OF.h}{AF}=\dfrac{f.h}{d-f}=\dfrac{12.1}{36-12}=0,5(m)\)

   Chiều cao của ảnh là 0,5cm.

   - Xét \(\Delta A'B'F \sim \Delta OIF'\)

    Ta có hệ thức:

    \( \dfrac{A'F'}{OF'}=\dfrac{A'B'}{OI}=\dfrac{h'}{h} \Rightarrow A'F' =\dfrac{OF.h'}{h}=\dfrac{f.h'}{h}=\dfrac{12.5}{1}=6(cm)\)

   Suy ra: OA'= OF'+A'F' =12+6=18(cm)

   b) d=8cm

  Xét \(\Delta OB'F' \sim \Delta BB'I,\) ta có hệ thức:

   \( \dfrac{BB'}{OB'}=\dfrac{BI}{OF'}=\dfrac{d}{f}=\dfrac{8}{12}=\dfrac{2}{3}\) (1)

   Xét \(\Delta OAB \sim \Delta OA'B'\) , ta có hệ thức:

   \(\dfrac{AB}{A'B'}=\dfrac{OB}{OB'}=\dfrac{OA}{OA'} \Rightarrow \dfrac{h}{h'}=\dfrac{d}{d'}\)  (2)

 Từ (1) và 92) suy ra h'=3h=3(cm)

                                 d'=24(cm)