Vật lý 10 Bài 27: Cơ năng

2.1.1. Định nghĩa.

• Khi một vật chuyển động trong trọng trường thì tổng động năng và thế năng của vật được gọi là cơ năng của vật trong trọng trường (gọi tắt là cơ năng của vật). 

• Cơ năng của vật kí hiệu \({\rm{W}}\), theo định nghĩa ta có thể viết:

     \(W = {W_d} + {W_t}\)

     \(W = \frac{1}{2}m{v^2} + mgz\)      (1)

2.1.2. Sự bảo toàn cơ năng của  vật chuyển động trong trọng trường

• Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn

 \(W = {W_d} + {W_t}\) = hằng số

\(\frac{1}{2}m{v^2} + mgz\) = hằng số

2.1.3. Hệ quả

• Trong quá trình chuyển động của một vật trong trọng trường :

  • Nếu động năng giảm thì thế năng tăng và ngược lại (động năng và thế năng chuyển hoá lẫn nhau)

  • Tại vị trí nào động năng cực đại thì thế năng cực tiểu và ngược lại.

2.2.1. Định nghĩa.

• Cơ năng của vật chuyển động dưới tác dụng của lực đàn hồi bằng tổng động năng và thế năng đàn hồi của vật : 

\({\rm{W}} = \frac{1}{2}m{v^2} + \frac{1}{2}k{\left( {\Delta l} \right)^2}\)

2.2.2. Sự bảo toàn cơ năng của vật chuyển động chỉ dưới tác dụng của lực đàn hồi.  

• Khi một vật chỉ chịu tác dụng của lực đàn hồi gây bởi sự biến dạng của một lò xo đàn hồi thì  cơ năng của vật là một đại lượng bảo toàn :

\({\rm{W}} = \frac{1}{2}m{v^2} + \frac{1}{2}k{\left( {\Delta l} \right)^2}\) = hằng số

• Hay :

\(\frac{1}{2}m{v_1}^2 + \frac{1}{2}k{(\Delta {l_1})^2} = \frac{1}{2}m{v_2}^2 + \frac{1}{2}k{(\Delta {l_2})^2} = ...\)

• Chú ý : Định luật bảo toàn cơ năng chỉ đúng khi vật chuyển động chỉ chịu tác dụng của trọng lực và lực đàn hồi. Nếu vật chịu tác dụng của lực cản, lực ma sát,… thì cơ năng của vật biến đổi. Công của các lực cản, lực ma sát,… sẽ bằng độ biến thiên của cơ năng.

Bài 1:

Một vật được ném lên theo phương thẳng đứng từ một điểm A cách mặt đất một khoảng 4m. Người ta quan sát thấy vật rơi chạm đất với vận tốc có độ lớn bằng 12 m/s. Cho \(g = 10m/{s^2}\) .
a) Xác định vận tốc của vật khi được ném. Tính độ cao cực đại mà vật có thể đạt được
b) Nếu vật được ném thẳng đứng xuống dưới vói vận tốc bằng 4m/s thì vận tốc của vật khi chạm đất bằng bao nhiêu?

Hướng dẫn giải

• Chọn gốc thế năng tại mặt đất

a.

• Tại độ cao cực đại mà vật có thể đạt được: 

 \({W_{tmax}} = {\rm{ }}{W_{dmax}} \Rightarrow mg{h_{max}} = {\rm{ }}0,5m{v^2} \Rightarrow {h_{max}} = \frac{{{\rm{ }}{v^2}}}{{2g}} = {\rm{ }}\frac{{{{12}^2}}}{{20}} = 7,2m\)

• Cơ năng tại vị trí ném = cơ năng tại vị trí vật đạt độ cao cực đại

 \(mgh{\rm{ }} + {\rm{ }}0,5m{v_o}^2 = mg{h_{max}}\)
 \( \Rightarrow 10.4{\rm{ }} + 0,5{v_o}^2 = 10{\rm{ }} \times 7,2 \Rightarrow {v_o} = 8m/s\)
b. Cơ năng tại vị trí ném = cơ năng tại mặt đất
 \(mgh + 0,5m{v_o}^2 = 0,5m{v^2}\)

\(10.4 + 0,{5.4^2} = 0,5{v^2} \Rightarrow v = 4\sqrt 6 {\rm{ }}\left( {m/s} \right)\)

Bài 2:

Hai vật A và B được nối với nhau bằng dây không giãn qua ròng rọc cố định với \({m_A} = 300g;{\rm{ }}{m_B} = {\rm{ }}200g\) . Vật trượt không ma sát trên mặt phẳng nghiêng góc \(\alpha  = {30^o}\) . Lúc đầu A cách mặt đất h=0,5m. Bỏ qua khối lượng của dây nối và ròng rọc.
a. Xác định vật tốc của vật A và B khi A chạm đất.
b. Khi A chạm đất vật B tiếp tục chuyển động đi lên trên mặt phẳng nghiêng một quãng đường bằng bao nhiêu.

Hướng dẫn giải

• Vật A cách mặt đất là h. Khi A chạm đất vật A đi được quãng đường là h, vật B cũng đi được quãng đường là h.

• Độ cao của vật B so với mặt đất: \({h_2} = {h_1} + {\rm{ }}h.sin\alpha \)

• Chọn gốc thế năng tại mặt đất:

• Cơ năng của hệ lúc thả:

 \(W = {W_{oA}} + {W_{oB}} = {m_A}.gh + {m_B}.g{h_1}\)

• Cơ năng của hệ lúc vật A chạm đất

 \(W = 0,5{m_A}{v_A}^2 + {\rm{ }}0,5{m_B}{v_B}^2 + {\rm{ }}{m_B}g{h_2}\)

• Áp dụng định luật bảo toàn cơ năng cho hệ chuyển động không ma sát

 \( \Rightarrow {v_A} = {v_{B}} = \sqrt {\frac{{2gh({m_A} - {m_B}sin\alpha )}}{{{m_A} + {m_B}}}}  = 2m/s\)

• Khi vật A chạm đất vật B vẫn còn chuyển động do quán tính, nhưng chuyển động của vật B là chuyển động thẳng chậm dần đều.

• Cơ năng của vật B lúc vật A dừng lại: 

 \({W_{B}} = {\rm{ }}{m_B}g{h_2} + {\rm{ }}0,5{m_B}{v^2}\)

• Cơ năng của vật B lúc dừng lại: 

 \(W{'_B} = {m_B}g{h_{3}} = {\rm{ }}{m_B}.g({h_2} + {\rm{ }}x.sin\alpha )\)
(với x là quãng đường vật B đi thêm được)

• Áp dụng định luật bảo toàn cơ năng 

 \({W_B} = W{'_{B}} \Rightarrow x = 0,4m\)

Bài 3:

Vật khối lượng m=1kg trượt từ đỉnh của mặt phẳng nghiêng cao 1m, dài 10m, lấy \(g = 9,8m/{s^2}\) ; hệ số ma sát là 0,05
a. Tính vận tốc của vật tại chân mặt phẳng nghiêng.
b. Tính quãng đường mà vật đi thêm được cho đến khi dừng hẳn trên mặt phẳng ngang.

Hướng dẫn giải

• Cơ năng tại A: \({W_A} = mgh = 9,8\left( J \right)\)

• Trong khi vật chuyển động từ A đến B, tại B cơ năng chuyển hóa thành động năng tại B và công để thắng lực ma sát 

⇒  Áp dụng định luật bảo toàn chuyển hóa năng lượng
\( \Rightarrow {W_A} = {\left( {{W_d}} \right)_B} + A\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Với \(({W_d}) = 0,5m{v_B}^2;{\rm{ }}A =  - {F_{ms}}.l =  - \mu Psin\alpha .l\left( 2 \right)\)

• Từ (1) và (2)  \( \Rightarrow {v_B} = 3,1m/s.\)

• Tại điểm C vật dừng lại ⇒ toàn bộ động năng tại B đã chuyển thành năng lượng để thắng lực ma sát trên đoạn BC.

\(\begin{array}{l}
 \Rightarrow {({W_d})_B} = |{A_{BC}}| = \mu .mg.BC\\
 \Rightarrow BC = 10m.
\end{array}\)

Qua bài giảng Cơ năng này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

• Viết được biểu thức tính cơ năng của một vật chuyển động trong trọng trường.

• Phát biểu được định luật bảo toàn cơ năng của một vật chuyển động trong trọng trường.

• Phát biểu được định luật bảo toàn cơ năng của một vật chuyển động dưới tác dụng lực đàn hồi của lò xo.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lý 10 Bài 27 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Từ điểm M (có độ cao so với mặt đất bằng 0,8 m) ném lên một vật với vận tốc đầu 2 m/s. Biết khối lượng của vật bằng 0,5 kg. Lấy g = 10 m/s². Cơ năng của vật bằng bao nhiêu?

  • A. 2J
  • B. 4J
  • C. 5J
  • D. 8J

• Câu 2:

  Một vật nhỏ được ném lên từ một điểm M phía trên mặt đất; vật lên tới điểm N thì dừng và rơi xuống đất. Bỏ qua sức cản không khí. Trong quá trình MN

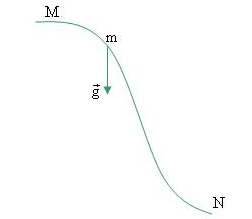
  • A. Động năng tăng
  • B. Thế năng giảm.
  • C. Cơ năng cực đại tại N.
  • D. Cơ năng không đổi.

• Câu 3:

  Một vật được ném lên theo phương thẳng đứng từ một điểm A cách mặt đất một khoảng 4m. Người ta quan sát thấy vật rơi chạm đất với vận tốc có độ lớn bằng 12 m/s. Cho \(g = 10m/{s^2}\) . Xác định vận tốc của vật khi được ném.

  • A. 5m/s
  • B. 8m/s
  • C. 10m/s
  • D. 4m/s

• Câu 4:

  Hai vật A và B được nối với nhau bằng dây không giãn qua ròng rọc cố định với \({m_A} = 300g;{\rm{ }}{m_B} = {\rm{ }}200g\) . Vật trượt không ma sát trên mặt phẳng nghiêng góc \(\alpha  = {30^o}\) . Lúc đầu A cách mặt đất h=0,5m. Bỏ qua khối lượng của dây nối và ròng rọc. Xác định vật tốc của vật A khi A chạm đất.

  • A. 1,5m/s
  • B. 3m/s
  • C. 2m/s
  • D. 4m/s

Câu 5- Câu 13: Xem thêm phần trắc nghiệm để làm thử Online 

Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lý 10 Bài 27 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Bài tập 4 trang 144 SGK Vật lý 10

Bài tập 5 trang 144 SGK Vật lý 10

Bài tập 6 trang 144 SGK Vật lý 10

Bài tập 7 trang 145 SGK Vật lý 10

Bài tập 8 trang 145 SGK Vật lý 10

Bài tập 1 trang 177 SGK Vật lý 10 nâng cao

Bài tập 2 trang 177 SGK Vật lý 10 nâng cao

Bài tập 3 trang 177 SGK Vật lý 10 nâng cao

Bài tập 4 trang 177 SGK Vật lý 10 nâng cao

Bài tập 1 trang 181 SGK Vật lý 10 nâng cao

Bài tập 2 trang 181 SGK Vật lý 10 nâng cao

Bài tập 3 trang 181 SGK Vật lý 10 nâng cao

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!