Vật lý 12 Bài 8: Giao thoa sóng

2.1.1. Thí nghiệm giao thoa sóng mặt nước

• Gắn hai hòn bi nhỏ vào thanh đàn hồi P và cho chúng chạm mặt nước.

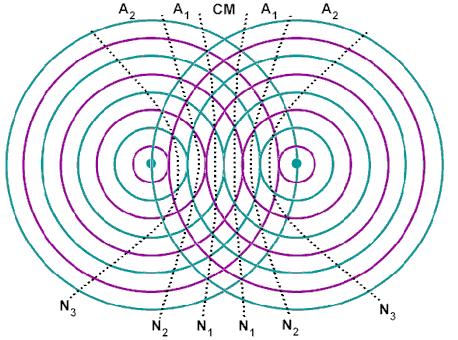
• Khi thanh dao động, hai hòn bi ở A và B tạo ra trên mặt nước hai hệ sóng lan truyền theo những hình tròn đồng tâm mở rộng dần và đan trộn vào nhau.

• Khi hình ảnh sóng đã ổn định, trên mặt nước có hai nhóm đường cong cố định: một nhóm có biên độ dao động cực đại xen kẽ với một nhóm khác tại đó mặt nước không dao động (biên độ cực tiểu).

• Hiện tượng trên gọi là hiện tượng giao thoa của sóng nước.

2.1.2. Nguồn kết hợp – sóng kết hợp

• Nguồn kết hợp: Là hai nguồn dao động cùng phương, cùng tần số, cùng pha hoặc có độ lệch pha không đổi theo thời gian (Δφ = const).

• Sóng kết hợp: Là hai sóng được tạo ra từ hai nguồn kết hợp.

• Trên mặt nước có sự lan truyền của hai sóng kết hợp và tại các điểm có sự gặp nhau của hai sóng kết hợp, ta có sự tổng hợp hai sóng.

2.1.3. Điều kiện để có giao thoa

• Điều kiện xảy ra giao thoa là 2 sóng kết hợp gặp nhau và dao động cùng phương.

• Hai sóng phải là sóng kết hơp: Tức là cùng tần số và có độ lệch pha không đổi theo thời gian.

2.2.1. Các phương trình sóng do nguồn A và nguồn B truyền tới điểm M

• Xét điểm M cách A và B các đoạn \(d_1; d_2\) (AB << \(d_1; d_2\)  để có thể coi biên độ các sóng truyền tới M là bằng nhau). Sóng từ A và B truyền đến M với vận tốc v.

• Giả sử 2 sóng A và B có cùng phương trình dao động là: \(\small u_A=u_B= a cos \omega t\)

  • Điểm M cách nguồn A đoạn \(d_1\) , cách nguồn B đoạn \(d_2\) . 

  • Phương trình dao động tại M do sóng A truyền đến là:  \(u_{1M}=acos(\omega t-2\pi \frac{d_1}{\lambda })\)

  • Phương trình dao động tại M do sóng B truyền đến là: \(u_{2M}=acos(\omega t-2\pi \frac{d_2}{\lambda })\)

2.2.2. Độ lệch pha giữa hai sóng kết hợp

 \(\Delta \varphi =\left |(-2\pi \frac{d_2}{\lambda })- (-2\pi \frac{d_1}{\lambda }) \right | =\frac{2\pi }{\lambda }\left | d_1-d_2 \right |\)

⇔ \(\Delta \varphi =\frac{2\pi }{\lambda }\left | d_1-d_2 \right |\)

• Trong đó : 

  •  \(d=\left | d_1-d_2 \right |\) là hiệu đường đi của 2 sóng từ 2 nguồn đến điểm đang xét trong vùng giao thoa (m)

  • \(\small \lambda\): Bước sóng (m)

  • \(\small \Delta \varphi\) : Độ lệch pha của 2 sóng 

2.2.3. Phương trình dao động tổng hợp

\(u_M=u_{1M}+u_{2M}=acos(\omega t-2\pi \frac{d_1}{\lambda })+ acos(\omega t-2\pi \frac{d_2}{\lambda }) =Acos(\omega t+\varphi )\)

• Biên độ tổng hợp:  \(A_M=2a.\left | cos[\frac{\pi}{\lambda }.(d_2-d_1)] \right |\)

• Độ lệch pha của 2 sóng tại M:

     \(\Delta \varphi _M=\frac{2\pi}{\lambda }.(d_2-d_1)\)

•  Pha ban đầu của sóng tại M:
  \(\varphi _M=\varphi -\frac{\pi}{\lambda }.(d_1+d_2)\)

2.3.1. Dao động của một điểm trong vùng giao thoa:

• Cho 2 nguồn \(S_1\) và \(S_2\) có cùng f , cùng pha

• Phương trình dao động tại 2 nguồn : \(u_1 =u_2=Acos\omega t=Acos\frac{2\pi t}{T}\)

• Xét điểm M cách \(S_1\) và \(S_2\)  một đoạn : d1 = \(S_1\)M và   d2 = \(S_2\)M 

• Coi biên độ bằng nhau và không đổi trong quá trình truyền sóng .

• Phương trình sóng từ  \(S_1\) đến M :\(u_{1M} =Acos\frac{2\pi }{T}(t-\frac{d_1}{v})=Acos2\pi (\frac{t}{T}-\frac{d_1}{\lambda })\)

• Phương trình sóng từ \(S_2\) đến M :\(u_{2M} =Acos\frac{2\pi }{T}(t-\frac{d_2}{v})=Acos2\pi (\frac{t}{T}-\frac{d_2}{\lambda })\)

• Phương trình Sóng tổng hợp tại M :

\(u_M=u_{1M}+u_{1M}=A.\left [cos2\pi (\frac{t}{T}-\frac{d_1}{\lambda })+cos2\pi (\frac{t}{T}-\frac{d_2}{\lambda }) \right ]\)

\(u_M=2A.cos\frac{\pi -(d_1-d_2)}{\lambda }.cos2\pi (\frac{t}{T}-\frac{(d_1+d_2)}{\lambda })\)

• Biên độ dao động là :   \(A=2A.\left | cos\frac{\pi (d_2-d_1)}{\lambda } \right |\)

2.3.2. Vị trí cực đại và cực tiểu giao thoa

• Vị trí các cực đại giao thoa

  • \((A_M)_{max}=2a\Leftrightarrow cos[\frac{\pi}{\lambda }(d_2-d_1)]=\pm 1\)
    \(\Rightarrow \frac{\pi}{\lambda }(d_2-d_1)=k\pi\Rightarrow d_2-d_1=k\lambda , k\in Z\)
    \(k=0\Rightarrow d_2-d_1=0\) đường cực đại trung tâm.
    \(k=\pm 1\Rightarrow d_2-d_1=\pm .\lambda\) đường cực đại bậc 1.
    \(k=\pm 2\Rightarrow d_2-d_1=\pm 2\lambda\) đường cực đại bậc 2.

• Ví trí các cực tiểu giao thoa :

  • \((A_M)_{min}=0\Leftrightarrow cos[\frac{\pi}{\lambda }(d_2-d_1)]=0\)
    \(\Rightarrow \frac{\pi}{\lambda }(d_2-d_1)=(k+\frac{1}{2})\pi\)
    \(\Rightarrow d_2-d_1=(k'+\frac{1}{2})\lambda =(2k'+1)\frac{\lambda }{2},k'\in Z\)
    \(\bigg \lbrack\begin{matrix} k'=0\Rightarrow d_2-d_1=\frac{1}{2}\lambda \\ k'=-1\Rightarrow d_2-d_1=-\frac{1}{2}\lambda \end{matrix}\) đường cực tiểu thứ 1
    \(\bigg \lbrack\begin{matrix} k'=1\Rightarrow d_2-d_1=\frac{3}{2}\lambda \\ k'=-2\Rightarrow d_2-d_1=-\frac{3}{2}\lambda \end{matrix}\)  đường cực tiểu thứ2

• Tóm lại:

 \(\frac{\left | d_2-d_1 \right |}{\lambda }=\left\{\begin{matrix} k\Rightarrow M \ thuoc \ cuc \ dai \ bac \ k\\ k+\frac{1}{2}\Rightarrow M \ thuoc \ cuc \ tieu \ bac \ (k+1) \end{matrix}\right.\)

• Suy ra :

  • Hiệu đường đi = một số nửa nguyên lần bước sóng

  • Quỹ tích các điểm này là những đường Hypebol có 2 tiêu điểm là  \(S_1\) và \(S_2\) gọi là những vân giao thoa cực tiểu .

Giao thoa sóng là sự gặp nhau của hai hay nhiều sóng kết hợp trong không gian, trong đó có những điểm cố định mà tại đó biên độ sóng được tăng cường hay giảm bớt.

Bài 1: 

Tại 2 điểm \(S_1, S_2\) trên mặt nước có 2 nguồn dao đọng theo phương thẳng đứng với phương trình \(u_{S_1}=u_{S_2}=3cos(20\pi t-\frac{\pi}{3})(mm)\) tốc độ truyền sóng v = 25 cm/s. Một điểm M trong vuông giao thoa cách \(S_1, S_2\) các đoạn 11 cm và 12 cm. Tìm độ lệch pha của 2 sóng tới M và biên độ sóng tại M?

Hướng dẫn giải

\(v=25 \ cm/s; \omega 20\pi\Rightarrow f=\frac{\omega }{2\pi}=10Hz\)
\(\Rightarrow \lambda =\frac{v}{f}=\frac{25}{10}=2,5 (cm)\)

• Độ lệch pha của 2 sóng tới M.

\(\Delta \varphi _M=\frac{2\pi}{\lambda }(d_2-d_1)=\frac{2\pi}{2,5 }(12-11)\)
\(\Rightarrow \Delta \varphi _M=0,8\pi (rad)\)

• Biên độ sóng tại M:

\(A_M=2a.\left | cos [\frac{\pi}{\lambda }(d_2-d_1)] \right |\)
\(\Rightarrow A_M=2.3.\left | cos [\frac{\pi}{2,5 }(12-11)] \right |\)
\(\Rightarrow A_M=2.3.\left | cos (\frac{2\pi}{3 }) \right |=3 (mm)\)

Bài 2:

Trên mặt nước tại 2 điểm A,B cách nhau 15cm có 2 nguồn dao động cùng pha và cùng tần số 10Hz. Tại điểm M trong vùng giao thoa cách 2 nguồn các đoạn 22cm và 28cm, sóng có biên độ cực đại. Giữa M và đường trung trực của AB có 2 đường cực đại khác. Tìm tốc độ truyền sóng và số điểm cực đại, cực tiểu trên đoạn AB?

Hướng dẫn giải

• Ta có   : \((A_M)_{max}\)

• Giữa M và trung trực AB có 2 cực đại khác.

\(\Rightarrow M\in CD_3\Rightarrow d_2-d_1-3\lambda \Rightarrow \lambda =\frac{d_2-d_1}{3}\)
\(\Rightarrow \lambda =\frac{28-22}{3}=2(cm)\)

• Tốc độ truyền sóng:

\(v=\lambda .f=20(cm/s)\)

• Số điểm cực đại:

\(\left | k \right |< \frac{AB}{\lambda }=\frac{15}{2}=7,5\)
\(\Rightarrow -7,5< k7,5\Rightarrow k=-7;-6\)\(\Rightarrow\) có 15 giá trị \(k\in Z\Rightarrow\) có 15 điểm CĐ.

• Số điểm cực tiểu: \(\left | k+\frac{1}{2} \right |< \frac{AB}{\lambda }=7,5\)

\(\Rightarrow -7,5< k+\frac{1}{2}< 7,5\Rightarrow -8 ⇒ Vậy có 14 điểm cực tiểu trên đoạn AB.

Qua bài giảng Giao thoa sóng này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Mô tả được hiện tượng giao thoa của hai sóng mặt nước 

• Viết được công thức xác định vị trí của cực đại và cực tiểu giao thoa.

• Vận dụng được công thức để giải thích bài toán đơn giản về hiện tượng giao thoa.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lý 12 Bài 8 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Trong hiện tượng giao thoa sóng trên bề mặt chất lỏng, hai nguồn dao động theo phương vuông góc với mặt chất lỏng, cùng pha, cùng tần số 50 Hz được đặt tại hai điểm S1 và S2 cách nhau 9 cm. Tốc độ truyền sóng trên mặt chất lỏng là 1 m/s. Trên mặt chất lỏng số vân giao thoa cực đại là

  • A. 10
  • B. 9
  • C. 8
  • D. 7

• Câu 2:

  Trong thí nghiệm giao thoa sóng trên mặt nước hai nguồn cùng pha bước sóng 2cm. Hiệu đường đi của hai sóng truyền từ hai nguồn tới vân giao thoa cực đại thứ năm là

  • A. 10cm
  • B. 1cm
  • C. 5cm
  • D. 2,5cm

• Câu 3:

  Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe bằng 1,2mm và khoảng cách từ hai khe đến màn quan sát bằng 2m. Chiếu hai khe bằng ánh sáng đơn sắc. Biết khoảng vân quan sát được trên màn bằng 1mm. Bước sóng của ánh sáng chiếu tới bằng 

  • A. 0,48\(\mu\)m
  • B. 0,50\(\mu\)m
  • C. 0,60\(\mu\)m
  • D. 0,75\(\mu\)m

• Câu 4:

  Ở mặt nước, có hai nguồn kêt hợp A, B dao động theo phương thẳng đứng với phương trình \(u_A=u_B=cos20\pi t\)  (mm). Tốc độ truyền sóng là 30 cm/s. Coi biên độ sóng không đổi khi sóng truyền đi. Phần tử M ở mặt nước cách hai nguồn lần lượt là 10,5 cm và 13,5 cm có biên độ dao động là 

  • A. 2 mm
  • B. 1 mm.
  • C. 0 mm
  • D.  4 mm.

Câu 5- Câu 13: Xem thêm phần trắc nghiệm để làm thử Online 

Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lý 12 Bài 8 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Bài tập 8.3 trang 22 SBT Vật lý 12

Bài tập 8.4 trang 22 SBT Vật lý 12

Bài tập 8.5 trang 22 SBT Vật lý 12

Bài tập 8.6 trang 22 SBT Vật lý 12

Bài tập 8.7 trang 22 SBT Vật lý 12

Bài tập 8.8 trang 23 SBT Vật lý 12

Bài tập 8.9 trang 23 SBT Vật lý 12

Bài tập 8.10 trang 23 SBT Vật lý 12

Bài tập 1 trang 89 SGK Vật lý 12 nâng cao

Bài tập 2 trang 89 SGK Vật lý 12 nâng cao

Bài tập 3 trang 89 SGK Vật lý 12 nâng cao

Bài tập 4 trang 89 SGK Vật lý 12 nâng cao

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!