Cho 2 bình hình trụ thông với nhau bằng một ống nhỏ như hình dưới...

* Hướng dẫn giải

Đáp án D

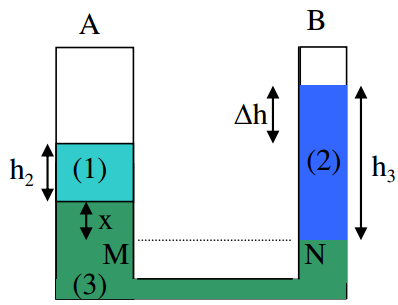
Xét điểm N trong ống B nằm tại mặt phân cách giữa nước và chất lỏng 3. Điểm M trong A nằm trên cùng mặt phẳng ngang với N. Ta có:

\( {P_N} = {P_M} \to {d_3}{h_3} = {d_2}{h_2} + {d_1}x\) (Với x là độ dày lớp nước nằm trên M)

\(\to x = \frac{{{d_3}{h_3} - {d_2}{h_2}}}{{{d_1}}} = \frac{{{{8.10}^3}.0,06 - {{9.10}^3}.0,04}}{{{{10}^4}}} = 1,2cm\)

Vì r₂ = 0,5 r₁ nên \( {S_2} = \frac{{{S_1}}}{{{2^2}}} = \frac{{12}}{{{2^2}}} = 3c{m^2}\)

Thể tích nước V trong bình B chính là thể tích nước chảy qua khoá K từ A sang B:

\(V_B =S_2.H = 3.H (cm^3)\)

Thể tích nước còn lại ở bình A là: 

\(V_A=S_1(H+x) = 12 (H +1,2) cm^3\)

Thể tích nước khi đổ vào A lúc đầu là: 

\(V = S_1h_1 = 12.18 = 126 cm^3\)

Vậy ta có: 

\(V = V_A + V_B => 216 = 12.(H + 1,2) + 3.H = 15.H + 14,4\)

\( \to H = \frac{{216 - 14,4}}{{15}} = 13,44cm\)

Vậy thể tích nước VB chảy qua khoá K là:

\(V_B = 3.H = 3.13,44 = 40,32 cm^3\)