Rút gọn các phân số sau về phân số tối giản: 60/72
Câu hỏi :
Rút gọn các phân số sau về phân số tối giản:
* Đáp án
* Hướng dẫn giải
Các phân số được gọi là tối giản khi phân số đó có tử và mẫu là hai số nguyên tố cùng nhau. Vậy để rút gọn các phân số (chưa phải là phân số tối giản) thì ta đi tìm ƯCLN của tử số và mẫu số, rồi lấy cả tử và mẫu chia cho ƯCLN của cả hai thì ta được phân số tối giản.
+ Rút gọn phân số
Ta có:
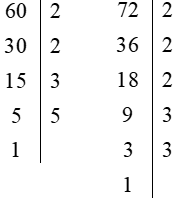
Do đó: 60 = 22 . 3 . 5 và 72 = 23 . 32
Các thừa số nguyên tố chung là 2 và 3, số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1
Suy ra ƯCLN(60, 72) = 22 . 31 = 4 . 3 = 12
Vậy
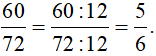
+ Rút gọn phân số
Ta có: 70 = 7 . 10 = 7 . (2 . 5) = 2 . 5 . 7
95 = 5 . 19
Thừa số nguyên tố chung là 5, có số mũ nhỏ nhất là 1
Khi đó: ƯCLN(70, 95) = 51 = 5
Vậy 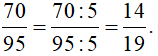
+ Rút gọn phân số 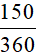
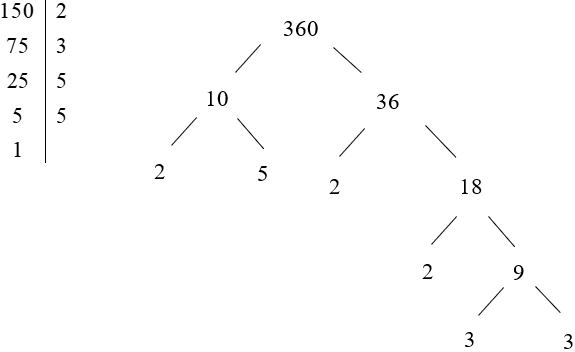
Do đó: 150 = 2 . 3 . 52
360 = 2 . 5 . 2 . 2 . 3 . 3 = 23 . 32 . 5
Các thừa số nguyên tố chung là 2, 3 và 5
Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1
Nên ƯCLN(150, 360) = 2 . 3. 5 = 30
Vậy 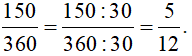
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SGK Toán 6 Chương 1: Số tự nhiên - Bộ Cánh diều !!
Copyright © 2021 HOCTAP247
