Tìm ƯCLN của hai số: a) 40 và 60; b) 16 và 124; c) 41 và 47

* Hướng dẫn giải

a) 40 và 60

Ta có: 

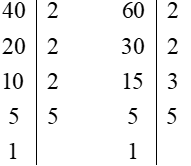
Do đó: 40 = 2 . 2 . 2 . 5 = 2³ . 5 

60 = 2 . 2 . 3 . 5 = 2² . 3 . 5

Các thừa số nguyên tố chung của 40 và 60 là 2 và 5

Số 2 có số mũ nhỏ nhất là 2; số 5 có số mũ nhỏ nhất là 1

Vậy ƯCLN(40, 60) = 2² . 5¹ = 4 . 5 = 20.

b) 16 và 124

Ta có: 16 = 2⁴ 

Lại có 

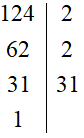
Do đó: 124 = 2 . 2 . 31 = 2² . 31

Thừa số nguyên tố chung của 16 và 124 là 2, với số mũ nhỏ nhất là 2.

Vậy ƯCLN(16, 124) = 2² = 4. 

c) 41 và 47

Ta có: số 41 chỉ có hai ước là 1 và 41 nên 41 là số nguyên tố

Số 47 chỉ có hai ước là 1 và 47 nên 47 cũng là số nguyên tố

Do đó 41 và 47 là hai số nguyên tố cùng nhau.

Vậy ƯCLN(41, 47) = 1.