Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng 6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhật, AD = 30cm. Số điểm cực đạ...

* Hướng dẫn giải

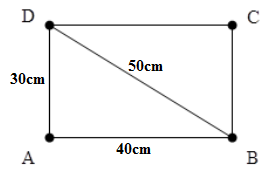
Áp dụng định lí Pitago ta có: DB = CA = 50cm

+ Số điểm cực đại giao thoa trên đoạn CD bằng số giá trị k nguyên thoả mãn:

\[\begin{array}{*{20}{l}}{\frac{{CB - CA}}{\lambda } \le k \le \frac{{DB - DA}}{\lambda } \Leftrightarrow \frac{{30 - 50}}{6} \le k \le \frac{{50 - 30}}{6}}\\{ \Leftrightarrow - 3,3 \le k \le 3,3 \Rightarrow k = - 3; - 2;...;3}\end{array}\]

Có 7 giá trị của k nguyên thoả mãn nên có 7 cực đại giao thoa

+ Số điểm đứng yên trên đoạn CD bằng số giá trị k nguyên thoả mãn:

\[\begin{array}{*{20}{l}}{\frac{{CB - CA}}{\lambda } - \frac{1}{2} \le k \le \frac{{DB - DA}}{\lambda } - \frac{1}{2}}\\{ \Leftrightarrow \frac{{30 - 50}}{6} - \frac{1}{2} \le k \le \frac{{50 - 30}}{6} - \frac{1}{2}}\\{ \Leftrightarrow - 3,8 \le k \le 2,8 \Rightarrow k = - 3; - 2;...;2}\end{array}\]

Có 6 giá trị của k nguyên thoả mãn nên có 6 điểm đứng yên.

Đáp án cần chọn là: D