Đề thi thử THPT chuyên Lam Sơn - 2021Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đâu đoạn mạch AB mắc nối tiếp gồm điện trở R không đổi và cuộn cảm thuầ...

* Hướng dẫn giải

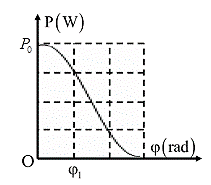
Từ đồ thị ta có:

Khi \[\varphi = 0 \to {P_{ma{\rm{x}}}} = {P_0} = \frac{{{U^2}}}{R}\,\,\,\,\left( 1 \right)\]

Khi  \[\varphi = {\varphi _1} \to P = \frac{3}{4}{P_0} = UI\cos \varphi = \frac{{{U^2}}}{{{Z^2}}}R\,\,\,\,\,\left( 2 \right)\]

Từ (1) và (2) ta suy ra: \[\frac{3}{4}\frac{{{U^2}}}{R} = \frac{{{U^2}}}{{{Z^2}}}R\]

\[ \Rightarrow 3{{\rm{Z}}^2} = 4{{\rm{R}}^2} \Leftrightarrow 3\left( {{R^2} + Z_L^2} \right) = 4{{\rm{R}}^2} \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\]

Lại có:  \[\tan {\varphi _1} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow {\varphi _1} = \frac{\pi }{6}\;rad\]

Đáp án cần chọn là: C