Người ta có nhiều nguồn âm điểm giống hệt nhau và cùng công suất. Ban đầu tại điểm O đặt 2 nguồn âm. Điểm A cách O một khoảng d có thể thay đổi được. Trên tia vuông góc với OA tại...

* Hướng dẫn giải

Trả lời:

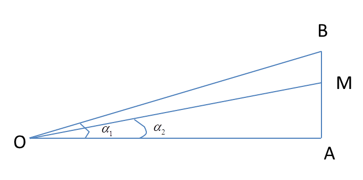
OA = d m

AB = 6 m

AM = 4,5 m

\[\tan = \tan \left( {{\alpha _1} - {\alpha _2}} \right) = \frac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 + \tan {\alpha _1}\tan {\alpha _2}}}\]

\[ = \frac{{\frac{6}{d} - \frac{{4,5}}{d}}}{{1 + \frac{6}{d}.\frac{{4,5}}{d}}} = \frac{{1,5}}{{d + \frac{{27}}{d}}}\]

Theo BĐT Cosi, ta có:

\[d + \frac{{27}}{d} \ge 2\sqrt {27} = 2.3\sqrt 3 \]

\[ \to d = 3\sqrt 3 m\]

Do đó:

\[OM = \sqrt {{{\left( {3\sqrt 3 } \right)}^2} + 4,{5^2}} = \frac{{3\sqrt {21} }}{2}m\]

Ta có:

\[{L_A} - {L_M} = 10\log \frac{{{I_A}}}{{{I_M}}}\]

\[ \Leftrightarrow 40 - 50 = - 10 = 10\log \frac{{{I_A}}}{{{I_M}}}\]

\[ \Rightarrow \frac{{{I_A}}}{{{I_M}}} = 0,1\]

Mặt khác:

\[\left\{ {\begin{array}{*{20}{c}}{{I_A} = \frac{{2P}}{{4\pi R_A^2}}}\\{{I_M} = \frac{{\left( {x + 2} \right)P}}{{4\pi R_M^2}}}\end{array}} \right.\]

\[ \to \frac{{{I_A}}}{{{I_M}}} = \frac{2}{{x + 2}}\frac{{R_M^2}}{{R_A^2}}\]

\[ \to \frac{{{I_A}}}{{{I_M}}} = \frac{2}{{x + 2}}\frac{{{{\left( {\frac{{3\sqrt {21} }}{2}} \right)}^2}}}{{{{\left( {3\sqrt 3 } \right)}^2}}}\]

\[ \to \frac{{{I_A}}}{{{I_M}}} = 0,1\]

\[ \to x = 33\]

Đáp án cần chọn là: D