Cho tứ diện ABCD. Gọi E,F,G là các điểm lần lượt thuộc các cạnh AB,AC,BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?

* Hướng dẫn giải

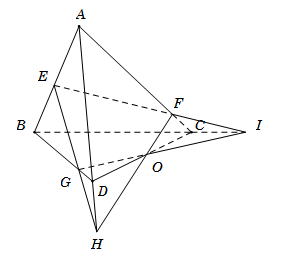
Trong\[mp(EHI)\],  gọi\[O = HF \cap IG\] Ta có

● \[O \in HF\] mà \[HF \subset \left( {ACD} \right)\] suy ra \[O \in \left( {ACD} \right)\].

● \[O \in IG\] mà \[IG \subset \left( {BCD} \right)\] suy ra \[O \in \left( {BCD} \right)\]

Do đó \[O \in \left( {ACD} \right) \cap \left( {BCD} \right)\] (1)

Mà \[\left( {ACD} \right) \cap \left( {BCD} \right) = CD\](2)

Từ (1) và (2), suy ra \[O \in CD\]

Vậy ba đường thẳng CD,IG,HF đồng quy.

Đáp án cần chọn là: B