Cho hình hộp ABCD.A′B′C′D′. Gọi M là điểm trên cạnh AC sao cho AC=3MC. Lấy N trên cạnh C′D sao cho C′N=xC′D. Với giá trị nào của xx thì MN//BD′.Ta có: M là điểm trên cạnh AC sao ch...

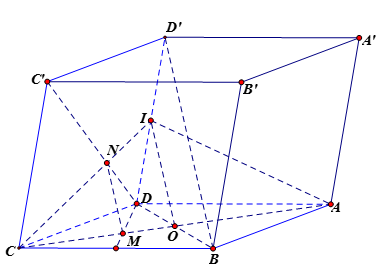
Ta có: M là điểm trên cạnh AC sao cho AC=3MC. Nên M là trọng tâm của tam giác BCD.

Gọi O và I lần lượt là trung điểm của AC và DD′. Khi đó ta có: \[BD'\;//\;\left( {IAC} \right)\]

Trong \[\left( {CDD'C'} \right)\] gọi\[N' = CI \cap C'D\] Suy ra N′ là trọng tâm tam giác CDD′.

Do đó: \[\frac{{CM}}{{CO}} = \frac{2}{3} = \frac{{CN'}}{{CI}} \Rightarrow MN'\;//\;OI\] mà\[OI\;//\;BD'\] nên\[MN'\;//\;BD'\]

Vậy\[N' \equiv N\] và\[x = \frac{2}{3}\]